RE: Kangaroo or Lion?

It’s a great pleasure for me to present the following comment to the post “Kangaroo or Lion?” from the 23rd of April, 2012, and to the further discussion, by IGM Petko Petkov

VARIATIONS OF ONE THEME

Igm PETKO PETKOV

Problem No. 4 is a very interesting work from Julia! My congratulations to her, about this nice h#2 whose mechanism is very rich and many modifications are possible here! Julia`s opus provokes also some important theoretical questions which deserve attention in practical aspect. (By the way, I accept Diyan`s proposal to change w.Pe5 with bl. Pe5).  

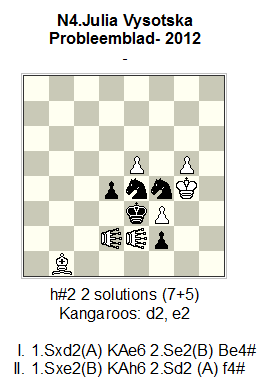
The author defines the thematic complex so: “Zilahi, Umnov, Critical KA-moves, cycle AB-BA of black self-block moves, creation of anti-batteries”.

OK, but here is needed to add: “Line-opening for white Kangaroos after black S-moves”.  

The main theme of Julia`s problem is possible to define so: “A black piece “X” blocks square around the black King and simultaneously opens line for white piece “Y” (from Hoppers-type). “Y” makes a critical move and then White creates an anti-battery and gives mate”. 

This complex, which reminds a classical “Indian theme”, is sufficiently difficult and interesting and it can be an independent theme in many other problems.

Therefore, I recommend to the readers to apply this theme in theirs own compositions, using different fairy pieces from Hopper`s type! 

But let we return again to No. 4. Here the author marks also other motives: cycle AB-BA of black moves and theme “Zilahi”. A special attention deserves the question about “Zilahi”. In my opinion, here we have only “Half-Zilahi” (we can say also “Partial Zilahi”)! 

My argumentation: here the mates follow after play of anti-batteries. But every anti-battery is constructed from two pieces: forward battery-piece (every kind of piece can execute this function) and rear battery-piece (only Hopper-piece can execute this function). For example: in I solution: I. 1.Sxd2(A) KAe6 2.Se2(B) Be4# the forward piece is the white Bishop but the rear piece is the white Kangaroo. The joint play of these figures follow to mate.

But attention! Here Black captures only one of these pieces – white Kangaroo! Therefore there is only “half” Zilahi effect. A whole Zilahi-effect would be possible only if Black captured the both white battery-pieces!

This argumentation must be valid also for standard direct or indirect batteries.

Two Kangaroos, or only one?

According to Seetharaman`s proposal 

seetharaman says:

April 23, 2012 at 9:13 pm

With the experts joining, this discussion is proving to be very interesting and educative. I have one question for the experts:

Suppose in Version 4, we remove Kangaroo e2. Now the problem can be twin (a) Diagram. (b) Move d2 to e2. The theme, play and content are unchanged. Would you prefer the twin setting with one Kangaroo less, or use two white Kangaroos for “multi solution” form ?Similar twinning possible for version 4.1 also.

N 4 can be modify to the following version – 4A :

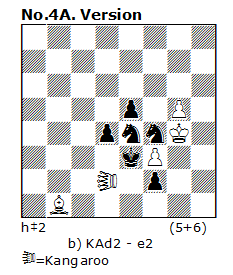
Here we have of course one Kangaroo less but there is in N 4A no “Half-Zilahi”. In my opinion here the choice between N 4 and N 4A can be a subjective estimate of author. 

Myself I think that the version with both Kangaroos and 2 solutions is better. Speaking for economy as the main principle in Chess composition, we cannot perceive this principle as a fanatic postulate which always should be interpreted as much as possible strictly. Between two Kangaroos in N4 exists a functional thematic subordination and it is not desirable to break this important effect which have also aesthetical value. 

Whether the Lion is better?

seetharaman says:

April 22, 2012 at 5:35 pm

Excellent imagination to show different effects with the similar settings of Nos.4 and 6. Can No.4 be more economical if Lions are used instead of Kangaroo.?

Julia`s answer:

About the Lions: Yes, I can take off the white pawns (e5, g5) in case of Lions, but at the same time I won’t need to block the squares e2/d2 on the blacks’ second move. So, have to find some other idea for this move.For now I’ve composed 2 versions of the problem No.4 – with Lions (4.1) and with neutrals: Bishop-Lion and Rook-Lion (4.2).Of course, some more motivations are possible to the black knights on the 2nd move.

I quite agree with Julia’s opinion that in this scheme the application of Lions instead of Kangaroo changes thematic complex. N 4.1 and N 4.2 are good problems of course but here exist also some important theoretical & practical questions.

At first it is possible, for example, to change the “Queen”-Lions in 4.1 with Rook-Lion and Bishop-Lion without any other thematic modifications – Version N 4B. 

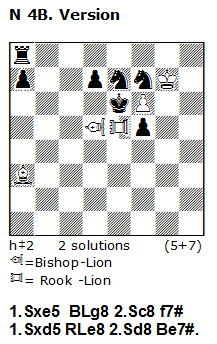
A simple rule, which have also subjective character: We should use always Rook-Lion(s) and Bishop-Lion (s) if the use of Queen-Lion (s) is not needed!  

The same rule is valid also for Kangaroos! We can define therefore three kind of Kangaroos: Queen`s Kangaroo (the well known standard type) , Rook-Kanagoo (plays only on Rook-lines) and Bishop-Kangaroo (plays only on Bishop-Lines). 

Therefore, in N4 we can change both Queen`s Kangaroos with theirs modifications: N 4C

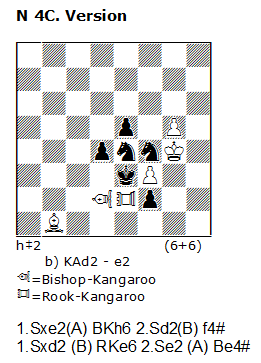
But what says the solver?

Changing Queen`s Lion or Queen`s Kangaroo with theirs slighter analogs, we submit an economy principle. OK. But this “thrift of power” has also negative effect.

As common conclusion we can say, that all pieces from type “Hoppers” are figures with rather limited mobility. Often on a diagram such pieces even cannot play, as Bishop-Kangaroo on the square “d2” in position 4C, for example. Here also Rook-Kangaroo on “e2” is almost immovable – it can play only on “e5”. In our basic problem – N 4 from Julia, every white Kangaroo has only one move: KAd2 – to g2, and KAe2 – to h5.

Such strong limited or full limited mobility of Hoppers in every case means an easy solution, of course, if the “move-distance” is short (2 moves) and the position is not heavy. Such compositions are a “facile drink” for the solvers, from other side, the strong limited mobility of Hoppers is obviously a negative fact in aesthetical attitude.

In my opinion, all these negative effects in one or in other degree exist in problems with short number of moves and especially – in help-genres. 

In this relation I can make the following general recommendation: if it is possible, compose Your problems in 2,5, 3 or more moves, in which yours Hopper –pieces have more possibilities for play. An interesting chance in this aspect is application of neutral or half-neutral pieces.