The Wonderful Genre PARRY SERIES by Petko A. Petkov

The Wonderful (new genre) Parry Series

(New edition of the article published in StrateGems No.51, 2010,
with a gratitude to Mr.Geoff Foster for the language correction)

IGM Petko A. Petkov

Dedicated to the memory of Dan Meinking, the inventor of Parry Series.

I. Introduction

One of the most interesting fairy inventions in the last few years is the so called “Parry series-mover”, by Dan Meinking. The first article, Parry Series: A New Frontier, dedicated to this problem type was published in the July-September issue of StrateGems (SG47), with twelve originals. That same issue featured seven additional parry series-movers in the Series-Movers & Stalemates column. In describing this wonderful new idea, Dan was assisted (with additional originals and cook-finding) by his colleagues: Kevin Begley, Mark Kirtley, Mike Neumeier , Kostas Prentos, George Sphicas and Raša Tomašević.

The first thematic tournament for Parry Series problems (Pser) was announced in November 2009 by the Good Companions (the informal association of U.S. composers) and it was a very interesting event with great success. The results of this “Quick Composing Tourney” (GCQCT) were published in SG 50/2010. Of course, very important was the fact that Meinking‘s invention was actively discussed on the popular Mat Plus website.

A powerful stimulus to Pser was given by Thomas Maeder while the GCQCT was still under way. He upgraded the Popeye solving program (version 4.55) for all Pser types and now it is possible to test (fully or partially) almost all possible kinds of such problems.

In this article I accentuate some important theoretical and practical ideas (and questions), connected with this new fairy condition. My conclusions are subjective of course. However, I think that at this moment, when Pser-compositions are being actively studied, and problems are being composed, each new article can be interesting and useful in some way.

This is the first of two planned articles. The second will be dedicated to Pser having fairy pieces and fairy conditions.

In writing this article, I was helped by Meinking‘s original article, my personal system for composing and analysis “PAPGS”, results from GCQCT and the last Version 4.55 of Popeye. As I always do in my articles, I will share my conclusions and proposals for the present and for the future possibilities in composing and checking Pser problems.

II. Definition

This is the original definition by its inventor, Dan Meinking: A parry series-mover differs from a standard series-mover prior to the last move as follows:

1. the series-side may give check during the series;
2. when checked, the idle-side must immediately parry the threat;
3. a parry-move may be helpful or defensive, depending on the problem-type;
4. after a check-and-parry, the series-side continues the series.

For simplicity, parry series-movers are denoted as: pser.*. When Popeye was upgraded, the form phser.* was also implemented to accommodate less-common problem types with helpful parries.

Every Pser problem combines two stipulations:

Part 1 – Pser, which indicates the special series play with participation of both sides according to the author’s definition;

Part 2 – the kind of problem, according to well known stipulations, which can show direct play (n#, n=, s#, s= r#, r=, etc), help play (h#, h=, h==, etc) or mixed play (hs#, hs=, hs= =, etc).

The structure of Pser is complicated and interesting when compared to traditional series-movers. An analogy with other fairy conditions, which also use “checks” for provocation of some effect, is possible, but not essential. Parry series is an original invention which does not copy old ideas.

Speaking in general about series problems, it would probably be best to clear up again the specifics of the play of these problems, having in consideration their structure and also some terminologically special features of this genre.

According the T.R.Dawson‘s definition, a series problem in “N” moves is a composition in which one side makes N-1 single and consecutive half-moves, and only on the last – Nth move do both sides play, realizing the final stipulation. Therefore this last Nth move is a complex move, formed by 2 half-moves – of White and Black. But by the enumeration of moves in a classical series problems there are no sense of which move is a half-move (one-side moves) and which move is “full- move” – a compound of 2 half-moves. If we write series h#10 – we accept that there are 9 half-moves by the side which makes the series and 1 “full move”, a compound of 2 half-moves. Such “equalization” of the terms does not seem normal, of course, but it is a tradition.

In other words, every traditional series problem in N moves has N -1 + 2 = N+1 half-moves. Only problems with one-sided series play in N moves (for example – ser d#10) have exactly N half-moves.

A Parry series problem in N moves is also created by half-moves but these half-moves are realized by both sides and many times – in different stages of the solution. Therefore, the common number of half moves is bigger here than in standard series problems and this is a very charming and important plus of Pser compositions! For example, an interesting question is: what is the fewest number of half- moves in a Pser-h#8? The correct answer is 10. But why? Some elementary schemes are needed to be shown here.

___________________________________________

In N1 we have a simple ser-h#6 with solution: 1 – 5.c1R! 6.Rb1 Sc2#. Here N=6, and the number of half-moves is N+1=7. An interesting thing is that Popeye will solve this problem also as Pser.h#6 (or even as Phser.h#6!) with the same solution! However, we can’t say that N1 is also a Pser.h#6, because here there are no  parry moves by White. Therefore, the author’s definition is not fulfilled!

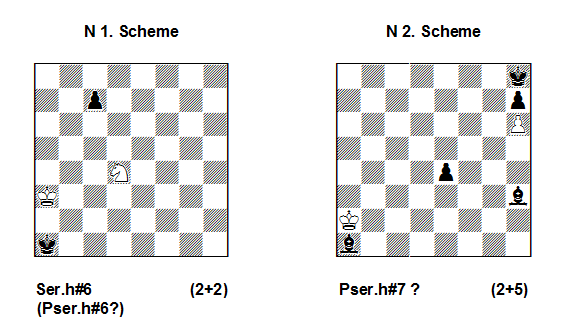
The availability of a minimum of one parry half-move from the idle-side, in my opinion, is an obligatory element of a Parry series problem! In other words, we must have two half-moves: a parry half-move, which parries a check, and the last, final half-move, which gives mate, stalemate, etc.

Thus, the minimal number of black and white half-moves in a Pser.h#8 is N+2 = 8 single black half-moves +2 white half-moves (1 parry-half move + 1 mating half-move) = 10 half-moves!

Another interesting question is provoked by scheme N2: 1.Be6 + Ka3 2.Bb2 + Kb4 3.Bc3 + Kc5 4.Bd4 + Kd6 5.Be5 + Ke7 6.Bf6 + Kf8 7.Bg7 + hxg7 #. But is it a real Pser.h#7 ? My answer is: no, because here we don’t have a series of black moves, i.e., every black half-move is a checking move after which follows White’s half-move. The number of black and white half-moves equals 7! Thus, the stipulation for N2 should be h#7, with a condition that Black must check. The solution is the same.

A parry series problem requires a series of half-moves by Black or White. The following also applies: if the number of all half-moves for the side which realizes the series is “X”, and the number of parry half-moves from the  idle-side is “Y”, then X>Y (X is greater than Y).

Obviously, the higher the number of half-moves on both sides, the more strategy can be applied. However, if X and Y are too close, often the result is a somewhat mechanical play, since fewer pieces on both sides are involved. Thus the value of X and Y will be defined based on the thematic complex, aesthetic requirements and economy.

III. Examples 

Part three of the Pser definition says: “A parry-move may be helpful or defensive, depending on the problem-type”.

A defensive parry-move appears in direct stipulations such as: #n, s#n, r#n, etc. For example, in a Pser.s#n, every parry move has two simultaneous functions: a) defend the enemy check, b) defend with the goal of preventing action from the other side, or more concretely – to avert the end result.

A helpful parry-move is a very interesting phenomenon, because it can exist not only in problems with help co-stipulations (h#, h=, h= =, etc), but also in some kinds of problems with direct co-stipulations (#n, s#n, r#n, etc). A helpful parry-move also has two simultaneous  functions: a) defend the enemy check, b) help the other side in the realization of the final goal.

Currently, based on the system used in StrateGems, the following designations are used for Pser problems:

• Pser.#n (or Pser.s#n, Pser.r#n, Pser. =n, etc) – all these kinds are possible to check with Popeye using a stipulation: Pser-#n (or Pser-s#n, Pser -r#n, Pser-=n, etc). 
• Pser.h#n (or Pser.h=n, Pser.h==n, etc) – all these kinds are possible to check with Popeye using a stipulation: Pser-h#n (or Pser-h=n, Pser-h==n, etc). 

There are also some mixed stipulations such as:

• Pser. hd#n – Pser help-directmate in n moves, Popeye Phser-#n.
• Pser. hs#n – Pser help-selfmate in n moves, Popeye Phser-s#n.
• Pser. hr#n – Pser help-reflexmate in n moves, Popeye Phser-r#n.

The difference in stipulations between Popeye and StrateGems is a “dot” in StrateGems and “dash” in Popeye. Thus in StrateGems we have Pser.#2 and in Popeye Pser-#2. Keep this in mind when using Popeye. Almost all other forms of Pser can be formulated using the cited symbols. Some new “exotic” forms will need new symbols as well as changes in Popeye.

Regarding the aesthetic criteria, it is necessary to formulate the following very important principle:

In a good Pser problem parry moves should be elements related to the thematic complex. Non-thematic parry moves, which exist in a problem only as mechanical instruments against opposing checks, are unacceptable. The quality of series moves, especially checking moves, is also important. The key should be, if possible, a non-checking move.

Thus far, many interesting Pser problems have been composed by its inventor – Dan Meinking. There is also an excellent collection of compositions which were honored in GCQCT (no fairy pieces or conditions were allowed there).

In N 3 we need to move the white Rook away from the a-file in order to allow the black King to move to a2-square. Thus: 1.Sa1! (1.Sd4?) 2.Qh7 3.Qb7+! – this checking-move allows White to make a defensive move – 3…Re4 and now the black series continues: 4.Ka2 5.Qb1 6.Rb2 7.Sb3 Ra4#.

In N 4 we have three parry moves by the white Knight: 1.h1Q! 2.Kh2 3.Qc1 + Sf4 4.Qc6 + Se6 5.Qc1 + Sg5 6.Qh1 Sf3#.

Very attractive is N 5 where we have two Excelsiors of which especially paradoxical is the white march by Pe2: 1- 5.g1Q! 6. Qg2+ e4! 7.Qb2+ Kc7 8.Qh2+ e5! 9.Qh7+ Kc8 10.Qf5+ e6! 11.Qc5+ Kd8 12.Qg5+ e7! 13.Qg8+ e8Q! 14.Qg1 Qe2#.

N 6 demonstrates a well known but very important and difficult for realization theme in this genre: reciprocal battery-creation R/B. As a nice additional motive, the black checking-moves are combined with Queen and Knight sacrifices: I.1.Qf7! 2.Qd7 + Re6 3.Sg7 + Kf6 4.Sh5 + Bxh5 5.Qf7 + Bxf7 6.d4 Rxe3 #; II. 1.Qh3! 2.Qf1 + Bf3 3.Sg4 4.Sh6 + Rxh6 5.Qh3 + Rxh3 6.e2 Bxd5 #. “A constructional triumph!” notes the judge, Dan Meinking.

A difficult and unusual thematic complex is shown in N 7 which at first sight seems insolvable: 1.Bf2! 2. Bh4 3.Bg5 4.Bh6 5.Bf8+ Kd8 6. Be7+ Kc7 7.Bd8+ Kb8 8.Bc7+ Ka7 9.Bb8+ Kb6 10. Ba7+ Ka5 11.Bb6+ Kb4 and now follows the black Bishop’s march in the opposite direction: 12. Bd8 13.Be7 14.Bf8 15.Bh6 16.Bg5 17. Bh4 18.Be1+ Bd2 – and now back to the other side again: 19. Bh4 20.Bg5 21.Bh6 22.Bf8 23.Be7 24.Bd8 25.Ba5+ Ka3 26.Bb4+ Kb2! 27. Bc3+ Bxc3 28.dxc3+ Kb1! 29.c2+ Kb2 30.c1B+!! Kc3 31.Ba3!! (tempo move!) d4#. An interesting try is 28…Kb3? 29.c2 30.c1S+ Kc3, but now Black has no waiting move and 31…d4# is not possible. A masterpiece: very fine two sacrifices by both Bishops, black “Phoenix” plus a tempo-move by the promoted Bishop!!

Only four men in N 8: I. 1.g1R! 2.Rg7 + Kb6 3.Rg6 + Kc5 4.Rg5 + Kd4 5.Rg4 + Ke3 6.Rg3 + Kf2 7.Rg2 + Kf1 8.Rh2 Sg3 #; II. 1.g1B +! Kb8 2.Ba7 + Kc7 3.Bb6 + Kd6 4.Bc5 + Ke5 5.Bd4 + Kf4 6.Be3 + Kg3 7.Bf2 + Kh3 8.Bg1 Sg3 #.

N 9 is another four-piece ensemble showing a double duel between black Pb7 and white King (on two adjoining files) and the black promoted Bishop and white King (on two adjoining diagonals) : 1.b6 + Ka4 1.b5 + Ka3 2.b4 + Ka2 3.b3 + Ka1 4.b2 + Ka2 5.b1B +! Kb3 6.Bc2 + Kc4 7.Bd3 + Kd5 8. Be4 + Ke6 9.Bf5 + Kf7 10.Be6+ Kf8 11.Bg8 12.Bh7 g7 #.

In N 10, Dan demonstrates an interesting and difficult complex with promotions of three(!) Queens: 1.g1Q + Kf3 2.Qa1 3.Qa8 + c6 4.h1Q + Ke3 5.Qxh3 + Kd2 6.Qd7 + c6xd7 7.c3 + Kxc3 8.Qc8 + d7xc8Q 9.Ka4 Qa6 #.

The first direct Pser threemover is N 11. After the key 1.Qg3+! we have three nice variations (which Popeye v4,55 shows as three different solutions): 1…Kf5 2.Bf1! 3.Bh3 #, 1…Ke6 2.Qc7 3.Bc8 #, 1… Kd4 2.Qe1 3.Qa1 #. Here we can presume, that the black K-moves are defensive, not help-moves, but obviously in such problems it is better if we have also thematic tries which accentuate the direct character of play and enrich the content. But such a goal is difficult to realize as more moves are needed, i.e., 4,5,6, etc.

In N 12 we see a very good try after 1.Re4? 2.Bf3 3.Rb4+ and if now 3…Ka6? follows 4.Rb5 5.Be2 6.Rb6#! However, Black refutes with a good defense 3…Kc8! The right way is: 1.Bf7! 2.Rh7 3.Bd5+! Kc8 4.Rd7 5.Be6! 6. Rc7# or 3…Ka6 4.Be6 5.Rh6 6.Bc8#. A difficult idea, with double reciprocal interchange of functions between white Rook and Bishop, which create and transform batteries! Unfortunately, here the four black Queens execute only technical functions but obviously it is impossible to eliminate this weakness. (Popeye v4.55 does not show try 1.Re4? or any tries in series problems.)

N 13 is a good selfmate example, with difficult solution, which shows fine reciprocal unpins by the white Bishops and return of Bg1: 1.Bb1! 2.Be3+ Kh5 3.Bc1 4. Bd3 5.Bxe2+ Kh4 6.Bd1 7.Be3 8.Bf2+ Kh3 9.Bg1 10.Bh5 11.Rg4 (zz) Rxg1#. A question: why not 1.Rg6+? Kh5 2.Rg5+ Kh4 3.Rg4+ Kh3 4. Bd3 5.Bxe2 6.Bc4 7.Bxe6 Rxg1#? Answer: The black King’s moves are defensive moves, therefore, after 1.Rg6+?, Black should not play 1…Kh5? but 1…Kxh7! .

A surprising black Indian theme is combined with four white promotions in N 14: 1.a8B! 2.Bc6 3.f8Q+ Ke6 4. d8Q 5.Qdd6+! Bxd6 6.g8Q+ Ke5 7.Kh2 8.Qg1 9.Bg2 10. Qf6+ Kxf6#.

When composing Pser Reflex problems (R#, R=, etc), keep in mind important aesthetical principles: The Reflex-tries in such problems are obligatory! There are three types of tries: a) Thematic (but not logical) tries, b) Logical tries, and c) Accidental tries (not related to the theme). Unfortunately till now Pser.r# has not been exploited enough, although, in many aspects, it is more difficult and richer than with Pser.s#.

N 15 is a light example with the main theme being destruction of the white battery combined with logical motives: 1.Qe2! 2.Rg7! (2.Rg8?, 2.Qh2+? Kxg5!) 3.Qh2+ Sh3 4. Qe5 5.Qg5+ Sxg5 6.Rg8 Sf7#. The tries which mate the black King are: 1.Qg3? (thr. 2.Rg7!) but 2.Qh4#; 1. Qf4? but 2.Qf6#;1. Qf3? (thr.2.Rg7! and 3.Oh4#) but 2.Qf6#; 1.Qe4? but 2.Qg6# etc.

Pser problems with mixed structure (help + direct) are a fertile field to find new ideas.

A little pearl (Aristocrat!) is N 16 with stipulation “Parry-series help-directmate in 7″ (or for short Pser-hd#7). Meinking’s definition is: “White makes a series of moves, Black parrying to help, leading to a directmate”. 1.Bf1 2.Rc4 + Sc7 3.Rg4 4.Ba6 + Bb7 5.Bf1 6.Bh3 7.Rg8 #. A very fine idea: the R/B battery is at first fully destroyed and then, after two switchbacks of the thematic pieces, recreated again in its original form! Problems of such types have a great future!

In the Pser help-self N 17 all black parry moves, including to the 14th move, are help-moves: 1- 5.d8S+! Kg7! 6.Kg5 7-9.f6+ Kh8+ 10.Kh6 11-12.f8R 13.Rf5 14.Sh5 followed by (typical for the HS# stipulation) selfmate in 1 move: 15.Sf7+ Sxf7#. The difference between this problem and N13 (Pser-s#11) is that in N13, the black parry moves were defensive answers to white checks!

In a Pser.hr#, until the N-1 move, we have help-play from both sides. White has to be careful, because the reflex obligation applies. In this field it is possible to compose good problems with logical play, based on the reflex obligation feature. N 18 is only a small example of this kind. The main plan is to play Rd2-Rd1 and after Rc1 Black must mate with Rb5#. The try 1.Rd2? fails to 2.Rd8#. The idea is to destruct the mating mechanism: 1.Rf2 – Rf7 – Rxa7+ Kb8 – Rd7 – Rd1 – Rc1 with mate Rb5# also fails as after 1.Rf2? follows 2.Rf8#. Analogically: 1.Re2? and 2.Re8#. Thus, the only right way is: 1.Rh6!! 2.Rxg6 3.Rg7 4.Rxa7+! – and now attention: as black parry moves should be help-moves, the answer is: 4…Kb8! (in a Pser-r#, where the parry moves are defensive, Black would answer with 4…Kxa7!) 5.Rd7 6.Rd1 7.Rc1 Rb5#.
This idea seems nice on first glance, but having only one black parry move – 4…Kb8 – is not enough.

N 19 is a version of N9 but with change of color and stipulation: 1. 1.g4 + Kh6 2.g5 + Kh7 3.g6 + Kh8 4.g7 + Kh7 5.g8B + Kg6 6.Bf7 + Kf5 7.Be6 + Ke4 8.Bd5 + Kd3 9.Bc4 + Kc2 10.Bd3 + Kc1 11.Bb1 12.Ba2 b2 #. Which version is better? In N19 we don’t have reflex-tries (as in N15). Therefore, N19 is only a rather formal reflex mate, in which, the reflex co-stipulation works only on the mating move!

IV. Special Notes

White series – Pserw

In this type of stipulation White moves first. The following combinations are possible: Pserw-h#n, Pserw-h=n, Pserw-h==, Pserw-h0-0 etc. Here the word Pserw means that White begins and realizes the series, Black answers with parry half-moves to the checks on his King, which becomes mate, stalemate, doublestalemate, etc, according to the kind of co-stipulation.

N 20 is a simple Pserw-h#9: 1.c3 + Kd5 2.c4 + Kd6 3.c5 + Kd7 4.c6 + Ke8 5. c7 6.c8=Q 7.Qc6 + Qd7 8.Qe6 + Re7 9.Qg8 #. Popeye does not provide for checking Pserw-h#n, but we can use an analogical stipulation: Phser-#9. (Similarly we can check N16 with Phser-#7, although the stipulation of N16 is Pser.hd#7.)

In my opinion, the symbols #7 and hd#7 mean that we have so called “direct problems” (“direct stipulations”), in a Pser form. It is important to clarify the meanings (and differences) between the direct problem, direct play, direct stipulation and help problem, help-play and help-stipulation. To me, the “direct problem” is one in which White attacks and Black defends, such as in #2, s#2, R#2, =2, R=2, etc. “Help problems” (help-stipulation) are compositions without confrontation between White and Black, i.e. both sides co-operate to reach the goal. Thus “help-direct” seems inappropriate. I prefer to use the designation Pserw-h#7 instead of Pser-hd#7. Special cases are Pser-hs# problems which are combinations of n-1 help moves and one direct (end) move.

Black series – Pserb

It is known from help-self problems (HSP), that there are compositions in which Black plays first. In such case the moves are marked with a fractional number, for example: HS#3.5 (Black begins the play followed by White to the Nth move, ending with a standard S#1.)

It is also possible to have Pser-hs# problems in which Black plays first. Here Black executes the series, White answers checks with parry half-moves. The play ends with a standard S#1 on the last two half-moves from Black and White. When Black begins the play, his moves are written first.

The following is important: If, in a Pser–hs#n, Black begins, the N-1 move is formed from two half-moves: first a black half-move, then a white half-move. On the last, Nth move, Black gives mate. Therefore here the S#1 final contains a white half-move from the N-1 move of the problem + a black mating half-move from the last Nth move of the problem!

In a Pser –hs#n, in which White begins, the S#1 final is realized from two half-moves – white and black, only on the last Nth move of the problem!

My proposal is to name these problems Pserb – hs# (hs=, hr#, hr=, etc) where the word Pserb means that Black begins play and executes the Series.

A simple example is N 21. 1.b1Q 2.Qd3 + Kg1 3.Qg6 + Kh1 4.Qc6 + Rxc6 + 5.Kb1 Rc2 6.Kxc2 #. Here only the last half-moves by Black and White execute a typical final for S#1. It is possible to check this problem with Popeye v4.55, but with condition Pser-hs#5.5.

Thus we can divide Parry series problems in two groups:

a) Pserw – in which White begins the play (series)

b) Pserb – in which Black begins the play (series)

To these main Pser stipulations one can add co-stipulations such as direct, indirect, mixed, etc.

V. Future Work

It is too early to speak of tendencies in the development of Parry series problems. Thus far, there are a relatively small number of compositions, mainly from the inventor Dan Meinking. Early tendencies were promotions and creation of batteries. It is a good beginning, and we can build on it. The things to look into are themes and ideas from other genres with specific application to Psers: destruction of batteries with different colors. A piquant idea is to create batteries after promotions (especially – with AUW!!) because it seems not so difficult in a play with series-character. Masking batteries also offer good opportunities. Other themes such as Grimshaw and Nowotny are applicable, but not with the standard battery motivation. One can try, for example, battery-creation after Grimshaw (Nowotny) with promoted Rook and Bishop.

Pins, unpins, half-pins, etc are possible. Line-clearance and Annihilation themes deserve interest. Pser is a good arena for the realization of systematical movements and duels between pieces of different colors.

I should emphasize that it is important to compose Pser problems with themes and ideas which are impossible to demonstrate in other genres!