Category: Theoretical Articles

Help-Self Problems with Black Series

By IGM Petko A. Petkov

In Memory of T.R. Dawson on the occasion of the 60th anniversary of his death

(Published in StrateGems #54 – 2011)

I. Introduction

This article is devoted to an interesting type of series-movers in which Black executes the series, but at the end White forces selfmate in one move! This type is rather different from traditional ser-s#n in which White executes the series from n-1 moves and at the nth move White forces selfmate in one.

Using Popeye, selfmate problems with Black series can be checked with stipulation ser-hs#n. Therefore, this denotation gives an impression that ser-hs#n is a modification from a well-known genre at present, hs#n. I tend to accept that the name “Series help-self mate in n moves” (ser-hs#n#) is better that the long name “Black plays a series of n-1 helpful moves so as to reach a position where there is a normal selfmate in 1”.

It is interesting that nobody can cite even ten old compositions with the stipulation ser-hs#n! My rather huge personal data base has but a few such opuses. Thus, I found it hard to illustrate this article. I asked for help from other fairy experts and they responded. I received problems from Bo Lindgren (thanks to Hans Gruber), Peter Harris and Cornel Pacurar. I also included several of my originals.

The stipulation ser-hs#n is an interesting and fresh genre which offers many new possibilities. (At present, the traditional series-genres, without fairy elements, are mostly exhausted.)

I should also mention the recently introduced Pser, which has a direct relationship with ser-hs#n. At the end of the article, I offer several new forms with rich practical possibilities and very surprising thematic nuances.

This article is dedicated to the memory of Thomas Rayner Dawson (1889-1951). In my opinion, we need a new, creative approach to Dawson’s heritage in Fairy Chess, especially series-movers. Many new forms and ideas are possible. In this article I will accent a limited number of novelties which figure in my work plans.

II. The Power of Black Series

Series-movers, in the classical form, ser-hs#n, were still in vogue in the first years following the World War II. (Black makes a series of “n” help moves and White makes the last, mating move.)

The series-mover is very old. Some such problems, known from Arabian manuscripts (XIII century), are cited by H.J.R. Murray in his A History of Chess (1962). I also know some older Arabian examples, but this special theme should be accented in a different article. As you see, we cannot ascribe 100% authorship to Dawson for series-movers. Nevertheless, his contribution is enormous because he formulated contemporary rules for them. His publication The Fairy Chess Review (1947) was a Fairy Bible. The ser-hs#n problems acted as a magnet for all fairy composers.

Some historical information is needed, especially for younger composers. It is important to know what the special features of series-movers are and also to know the classical tendencies.

We start with N1, a typical of Dawson’s miniature with excellent educational value. 1-7.Ke1 8.f1R 9.Rf2 10-16.Ka1 17.Ra2 Sb3#.

The stipulation ser.h=n, in which the mate is replaced with stalemate, appeared later (probably after 1950). The content of the earlier problems was rather simple. N2 1.Qh2 2.Kxg2 3-9.Kc1 10.Qc2 11.Qb1 12.Qa1 13.Kb1 Kd2=.

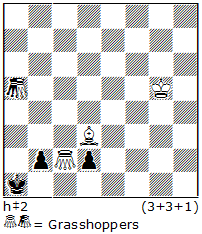
Before 1960, many compositions with the stipulation ser.h==n, were also published, some of them with fairy elements! N3 1.c6 2.Kc7 3.Kb8 4.Ga8 5.Gc8 6.Gc5 7.Gc7 8.c5 9.c4 10.c3 11.c2+ MAc6==.

III. Series Selfmates – a Natural Modification

As a natural modification of ser-hs#n, the stipulation ser-s#n arises early. In just two years, 1949 and 1950, according to my fairy data-base, twenty-five such problems were published, many of them cooked.

The first ser-s#ns were light compositions in the spirit of N4. 1.Rh6 2.Sc3 3.Qxd6 4.Bd2 5.0-0-0 6.Bb1 7.Qxa3+ Bxa3#. Development continued with the creation of masterpieces with a task character. The themes are mainly different promotions, especially AUW, double AUW, Super AUW, etc., often composed with neutral pieces.

N5 1.e8S 2.Sxf6 3.Sd5 6.f8Q 7.Qxf3 8.Qg2 13.f8B 14.Bxh6 15.Be3 18.h8R 19.Rxh4 20.Re4 25.h8Q 26.Qxb8 27.Qe5 28.b8B 29.Bxa7 30.Bc5 32.a8R 33.Rxa4 34.Rb4 39.a8S 40.Sab6 41.Sc4 42.Qxe2+ Sxe2#. A double white AUW!

N6 shows a neutral Super AUW with maximum economy of material 1.b8nB! 2.cxb8nG (nBf8) 3.nBxa3 (nPa7) 4.a8nQ 5.nQxg2 (nPg7) 6.g8nR 7.nRg6 8.h8nS+ nSxg6 (nRh1)#. A logical problem with good strategic motives is N7. The main plan is 1.Kg3 2.Kxh2 (Sb8) 3.b7+!? and now not 3…Kxb7 (Pb2)# but 3…Bxb7 (Pb2)+ 4.Kh3. After a long Pendel maneuver, Rg2 moves to a2. 1.Qf2 2.Rgg1 3.Qd4 4.Bc3 5.Ba5 6.Ra1 7.Ra2 8.Bc3 9.Ba1 10.Qg1 and now: 11.Kg3! 12.Kxh2 (Sb8) 13.b7+ Kxb7 (Pb2)#.

IV. A Pleasant Surprise

When was the first help-compel mate, with black series (ser-hs#n), published? Unfortunately, I don’t have the answer. I only know that few have been published.

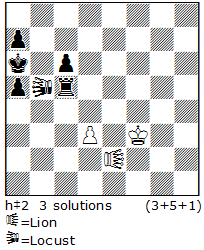
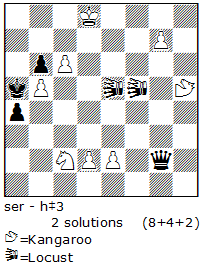
I would like to show you N8, a problem published not long ago. 1.Sed3! 2.d1Q 3.Qf3 4.Sf2! 5.g1Q 6.Qxh2 7.Sg4! 8.Qh4 9.Qe7 10.Se5! 11.Qff6. This ends the eleven-move series phase and is followed by a selfmate in one: 12.Bc4+ Sbxc4/Sexc4#. The content is rich with bS Rundlauf, two bQ promotions, two self-blocks and a creation of a black battery. This is a lot for just eleven moves.

Analyzing this composition we can define the main aesthetic criteria for a contemporary ser-hs#n# as:

A – Since the main content of the problem is in Black’s moves, the prime goal is to create (a surprising) mating mechanism culminating with the last phase (s#1). To achieve this, a sufficient number of black moves is needed, often ten or more.

B – The black series must have a thematic content or a combination of themes and ideas. The composer should also strive for a difficult solution.

In the following problems these criteria are executed to some degree.

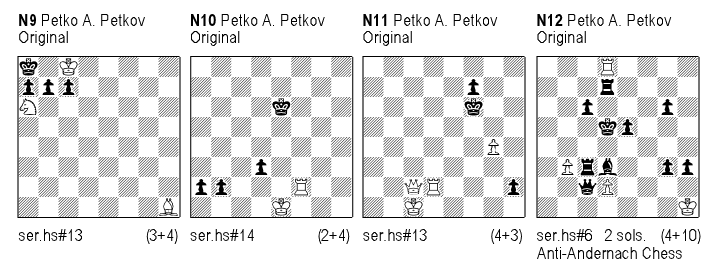
In N9, the black series shows two Excelsior’s, reciprocal unpins between black Pawns and a pseudo-switchbacks of black promoted pieces to b7 and c7. 1.c6! 2-6.b1R 7.Rb7! 8-12.c1Q+!. The black series ends and selfmate-in-one follows: 12…Sc7+ 13. Qxc7#.

It is interesting to note that Popeye solves this problem (and others of this kind) as a ser.hs#12, i.e., it disregards the last mating move although it is shown in the solution. In my opinion, the right stipulation here can only be ser-hs#13.

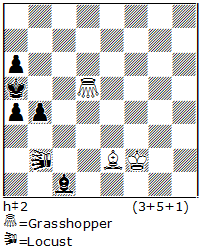
N10 demonstrates an interesting theme which seems novel. Here, Black creates one battery which cannot deliver mate. This battery is abandoned and a new battery is created, which mates. 1.b1S! 2.a1R! (battery is created) 3.Ra4 (battery is abandoned) 4.Rf4 5-7. Kh3 8.Rg4 9.Rg2 10-11.Kg1 12-13.Rh1 (a new battery is created) leading to the finale: 14.Rg2+! Kxg2#.

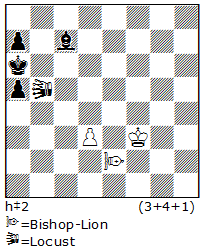
In N11, in the first phase, Black creates a B/Q battery: 1.Ke5 2-6.f1B 7.h1Q which is subsequently destroyed. A new, similar battery, is constructed on the opposite side of the board: 8.Qa8 9.Bc4 10.Ba2 11.Bb1 12.Qa1! and then 12…Qf5+ 13.Bxf5# with line clearance.

Using fairy elements (pieces, conditions, etc.) a composer can demonstrate a wealth of new, and sometimes unusual, ideas. Often, such problems are also hard to solve.

N12 1.Qxb3 (Ke4?) 2.Bb1=wB 3.Rc2=wR 4.Ke4 5.Rf7=wR Rxc6+ 6.Qxb1#, 1.Qxd2 (Kc5?) 2.Rc1=wR 3.Bc2=wB 4.Kc5 5.Rb7=wR Bxg6+ 6.Qxc1#. Line opening, Indian, Grimshaw on “c2”, unpins by the black Rook which opens line for Rd8.

The following is a quartet of hypermodern compositions by Peter Harris.

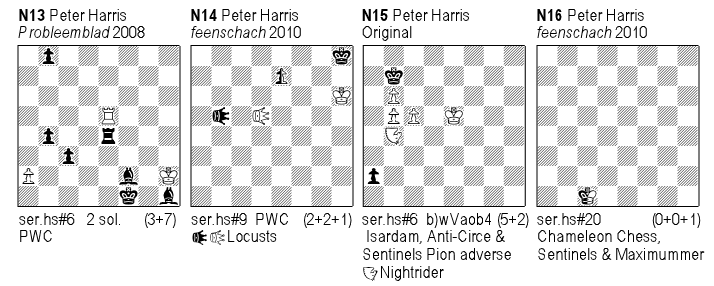
N13 1.b3 2.Ra4 3.Ra8 4.Rxa2 (+wPa8=wS) 5.Bxa8 (+wSh1) 6.Bg2 Sg3+ 7.Bxg3 (+wSf2), 1.Rg4 2.Bd5 3.Bg8 4.Bxa2 (+wPg8=wB) 5.Rxg8 (+wBg4) 6.Rh8+ Bh3+ 7.Rxh3 (+wBh8) #. Two nice promotions in S and B with specific PWC mates.

N14 1.nPe6 2.nPxd5 (+wLOe6) 3.LOxd5-e5 (+nPb5) 4.LOxe6-e7 (+wLOe5) 5.LOxe5-e4 (+wLOe7) 6.LOxe7-e8 (+wLOe4) 7.LOxb5-a4 (+nPe8=nLO) 8.LOxe4-f4 (+wLOa4) LOxf4-g4 (+bLOa3) zz 9.LOxg4-h4 (+wLOa4)#.

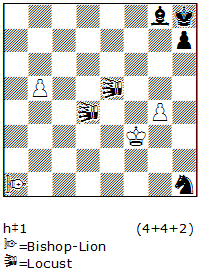
N15 a) 1.a1N 2.Nb3 3.Nd4 (+wPb3) 4.Nxb3 (bNb1) (+wPd4), Pd4 will prevent wK from moving, 5.Na3+ Nf6 (+bPb4). This defends against the check because the bP prevents bN from moving, 6.b3#. Pb4 no longer prevents bN from guarding e1-square. b) 1.a1VAO 2.VAOd4 3.VAOxb6 (bVAOb1) (+wPd4), without wPb6, the bK can now move to c7, while Pd4 prevents the wK from moving, 4.Kc7 (+wPb7 5.Kd7 (+wPc7) b8S!. This is not a check since b1-square is occupied by bVAO, a pinned piece under the circumstances, 6.Ke6 (+wPd7)#.

N16 1.nKd2 2.nKe3 (+bPd2) 3.nKd4 (+bPe3) 4.nKc5 (+bPd4) 5.nKd6 (+bPc5) 6.nKc7 (+bPd6) 7.nKb8 (+bPc7) 8.nKa7 9.nKb8 (+bPa7) 10.a5 11.nKa7 12.nKb8 (+bPa7) 13.e2 14.d1Q 15.Qa4=S 16.Sb6=B (+bPa4) 17.a6 18.Ba7=R 19.e1R nKc8 20.Re8=Q#.

V. Application of Pser

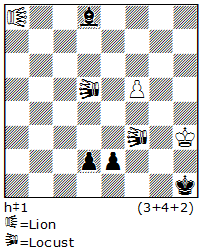
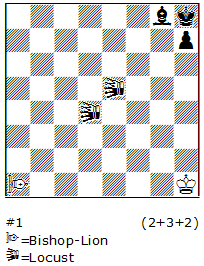
It is only logical to combine ser-hs#n (=, ==, etc.) with the Pser. Such problems we can designate as Pser-hs#n (used also by Popeye). I have paid attention to this opportunity in my article The Wonderful (new genre) Parry Series (SG51/2010), illustrating it with N17. 1.b1Q 2.Qd3+ Kg1 3.Qg6+ Kh1 4.Qc6+ Rxc6+ 5.Kb1 Rc2 6.Kxc2#. This setting can be checked with Popeye as Pser-hs#5.

N18 a) 1.Qc2+ Kh3 2.Qf5+ Rg4 3.Qd3+ Bf3 4.Qf1+ Kh2 5.Qf2+ Kh1 6.Kf1 Rg1+ 7.Qxg1#, b) 1.Qb6 + Rfd4 2.Qg6+ Kh1 3.Kf2 4.Kg3 5.Kh3 6.Qg3 Bg2+ 7.Qxg2#. A difficult fiver!

N19 a) 1.Kd8 2.Rd7+ Kc6 3.Rd6+ Kb7 4.Rd7+ Ka8 5.Re7 Qc8+ 6.Kxc8=, b) 1.Ke8 2.Re7+ Kf6 3.Re6+ Kg7 4.Re7+ Kh8 5.Rd7 Qf8+ 6.Kxf =. Perfect Chameleon-echo with four men.

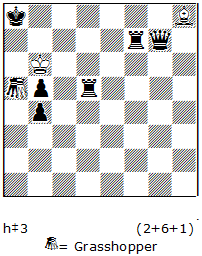
N20 1.Rc2 2.Kb2+ Kd7 3.Ka1 4.Rc7+ Ke6 5.Rc6+ Kf5 6.Rc5+ Kg4 7.h5+ Kg3 8.h4+ Kg2 9.h3+ Kh1 10.Rc1+ Rd1 11.Rb1 Rc1 12.Rxc1#. The long and dynamic play, with surprising maneuvers by both sides, ends with a model mate.

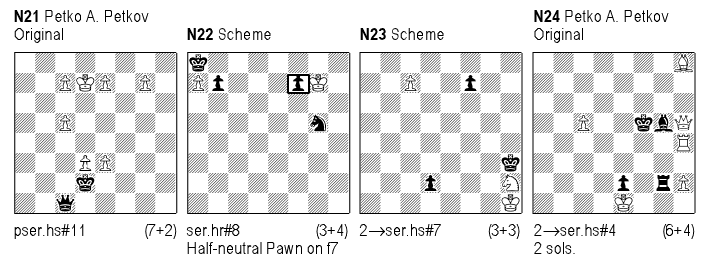
N21 is a task which shows three white R-promotions plus three annihilations of white Pawns with a goal of line openings for promoted Rooks. 1.Qxc5 2.Qxe3 3.Qh3+ Ke8 4.Qh8+ g8R 5.Qh5+ Rg6 6.Qb5+ Kd8 7.Qb8+ c8R 8.Qf4 9.Qf8+ e8R 10.Kxd3 Rd6+ 11.Qxd6 #. Great activity by the bQ (10 moves!), plus a model-mate.

VI. Other New Variations

I was planning to provide many new ideas, but due to personal matters, I had a limited time to work on them. Many problems which I started remain unfinished. I hope to provide additional insight at some later date.

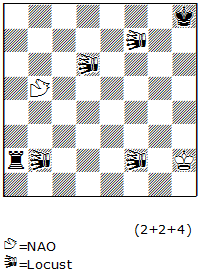
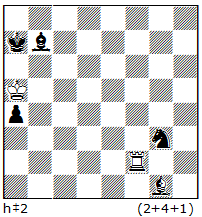
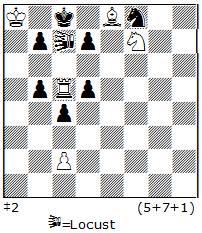
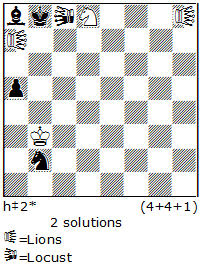
A) Reflexmates + Black series. Using the black series, one can compose many variations of reflexmates such as: ser-hr#n or ser-hr=n, ser-hr==n, ser-hr+n, Pser-hr#n, or Pser-hr=n, etc. In a ser-hr#n, Black plays a series of n-1 moves, then White forces r#1. The same rules apply as for a regular reflexmate, i.e., White is obliged to mate at any time during the black series, if possible. Aesthetically, such reflex-tries are obligatory. Semi-reflexmates are also possible. Unfortunately, Popeye is not yet programed to handle them, so it is difficult to compose them. An elementary example is N22. The try 1.bhPf5=nhP? 2.nhPf4=bhP 3.bhPf3=nhP 4.nhPf2=bhP 5.f1=nhQ with the goal of 5…Kh8 and 6.hnQf8=bhQ#, but here White must mate with 5…hnQf8=whQ#! Therefore Black must find another way to realize his Excelsior: 1.bhPf6=nhP! 2.nhPf5=bhP 3.bhPf4=nhP 4.nhPf3=bhP 5.bhPf2=nhP 6.f1=bhQ! 7.bhQb1=nhQ! and now 7…Kh8 8.nhQh7=bhQ#! And not 7.bhQd3=nhQ? 8.nhQd8=whQ#! Work with half-neutral pieces shows great promise.

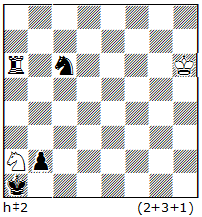
B) White + Black series. This is an interesting and promising new form. At first White makes a series of “x” half-moves, which we can call an introduction. After that Black makes its series of “y” moves as in a normal ser-hs#n (ser-hs=n, ser-hs==n, etc.). The stipulation in N23 is 2→ser-hs#7. White makes two moves, 1.c8R 2.Rf8!, followed by Black, who makes six moves, 1- 5.f1S 6.d1R followed by the finale 6…Rf3+ 7.Sg3#.

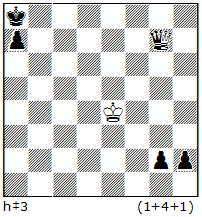
In N24, the introduction shows creation of a White Indian: 1.Bc3 2.Rd4!, followed by Black series: 1.Kf6 2.Bc1 3.Bb2 and follows s#1: 3…Re4+ 4.Bxc3 #. Similarly: 1.Rb4 2.Bd4 & 1.Kf4 2.Bd8 3.Ba5 Bg1+ 4.Bxb4#. Both sides provide rich thematic play with model-mates in economic construction.

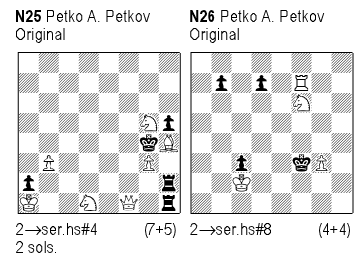
N25 1.Qd3 2.Qb1 & 1.axb1S 2.Sd2 3.Sf1 Se3+ 4.Sxe3#, 1.Sc3 2.Sb1 & 1.axb1B 2.Bc2 3.Bd1 Qf3+ 4.Bxf3 #. Reciprocal sacrifices by the wQ and the wS on b1 in the introduction, followed by promotions, Dentist-theme, creation and transformation of masked black batteries and Umnov.

C) White introduction + Pser. An interesting modification of Pser. Here the Pser-hs#n play follows White introduction.

(When checking with Popeye use: x→pser-hs#y , where “x” is the number of introductory moves and “y” is the number of black series moves. (Popeye exhibits the same flaw as mentioned before.)

The introduction should have thematic content and also be difficult to solve, otherwise, it is not desirable.

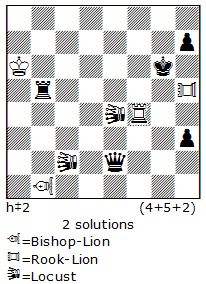
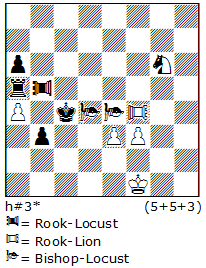
In N26, the introduction contains only two moves, which are hard to find: 1.Rf8 2.Rd8! White destroys its S/R battery, and then moves its Rook into an ambush. After the Pser play: 1- 3.d3+ Kd1 4.c2+ Ke1 5.d2+ Kf1 6.d1S 7.c1R! we have a selfmate in one: 7…Rd3+ 8.Se3#. The try 1.Rxd7? 2.Kd1, after the march of the c-Pawn (which is needed because of the cook), is 1-3.b3+ Kd1 4.c2+ Ke1, and the white King has no more parry-moves for moving to “e1”. Another analogy is that White destroys S/R battery while Black builds the S/R battery.

VII. The Future Work

I think there are some terminological problems when using the name series help-selfmate in “n” (as used by Popeye). I’m not sure it will be accepted as an official name. Other names are possible, of course, but a historical inevitability is the standardization of all fairy terms, names, and symbols which are used in programs and under diagrams. This work should be one of the most important duties of the WFCC. I am also hoping for a speedy incorporation of self-problems with black series into Popeye.

In regard to aesthetic criteria of help-compel mates, most of it was defined in my previous article in StrateGems (SG32), although additional work in this area is also possible.

Another area of interest is the Pser series (including the introduction element). Creative work is always an important element but fast computers will be needed for checking these problems.

My recommendation to composers is to start with schemes that incorporate fewer than 8 or 9 moves. More complex scheme will be difficult to verify. One can also work with black series (maximum 6-7 moves). The key here is to have a good thematic content.

---

BLOCK OF NEUTRAL BATTERY-PIECE (Part II) IGM PETKO PETKOV

---

See  Part I in the Theoretical Articles Category

III. WORK WITH LOCUSTS

Why we should pay a special attention to the Locust fairy piece, developing our main theme? Indeed, some examples were already shown in the first part of this article!

My answer is: although the Locust is not a new piece (its modifications, like Rook-Locust, Bishop-Locust etc. are well know in practice), I think that there’re arguments for even more complete examination of this piece in relation to this topic. More specifically:

a) We are talking about neutral Locusts, but the are not much used in practice, when the problems don’t contain any additional fairy conditions.

b) Many effects of these pieces are little known, and some of them, which will be discussed later, perhaps are very little used, or even never met until now.

c) In some modern genres – for example, HS# or HS= fairy problems, neutral Locusts are still poorly used and there is a huge practical reserve.

d) In theoretical approach it is interesting to examine a number of issues here, that are not clarified in the theory of fairy problems, meaning in reality, that the term “theory” is very relative in this arena. It is well known, that up to now such a theory – in a form of a serious, complete scientific and practical work – doesn’t actually exist.

e) The central theme of this article – block of neutral battery piece – has a particular importance, since exactly this motif, as it was already mentioned, interferes with the side which gets mate, to protect itself by escaping a neutral piece, which we have named “X”.

f) Since this article has a strong practical emphasis and is also planned for the wide range of readers, especially – beginners, many motifs here are explained with only a simple diagrams, which demonstrate the important basic effects the readers can apply in their work.

So, let’s continue with the series of examples, where Locust is a forward piece or rear piece in a different batteries or anti-batteries.

As a forward piece, neutral Locust can demonstrate an interesting effects – it opens the battery, but at the same time the side which is in defense captures the rear piece with the same neutral Locust and the goal can’t be reached immediately. Thus, blocking of piece “X” which is implemented by the own piece or by the piece of the other side, prevents the piece “X” from the capturing of the rear battery piece, destructing the battery. One such an example you’re already seen in the part I – problem No.6 – a fairy twomover, where “X” acted as a forward piece in the direct battery, but in No.7 – as a forward piece in the anti-battery, although there was just one solution.

Let’s continue a little bit with the examples of this type.

No.9. Petko A.Petkov

Educational example

In No.9 we can see that the battery is going to play. The battery is created by the following pieces: nLOb5 – forward piece, LIe2 – rear piece, Pd3 – a pawn, which has only technical functions from the first view, although without it it would be impossible to create our battery. At the beginning let’s try this idea for the solution: 1.Rc3 ~ 2.Rb3 nLOxb3-b2+? – but here we see already known defense by the black: 3.nLOxe2-f2+! – capturing the battery-piece LIe2.

It’s not difficult to guess, that white (for now we haven’t defined their first move) can block the square f2 — and everything will be fine. Thus we have: I. 1.Rc3! Kf2! 2.Rb3 nLOxb3-b2#! But the problem has 3 solutions — let’s see what’s going on.

Analogical ideas by the black Rook we can implement also with the moves: 1.Rc4 1.Rc2. But suddenly, the very important role here has exactly our pawn on d3!

First, let’s try: 1.Rc4 ~ 2. Rb4 nLOxb4-b3+? but 3. nLOxd3!! – white battery doesn’t exist anymore as the pawn d3, which is needed in this construction, is removed, and there’s no mate! Therefore we should here also block the square e3 with a white by analogy with the first solution, to make impossible a capture on d3: II. 1.Rc4 Ke3! 2. Rb4 nLOxb4-b3#! Analogically: III. 1.Rc2 Ke4! 2. Rb2 nLOxb2-b1#! – again the white King has blocked the square for the neutral Locust!

Now it’s a time to speak again about the white pawn, which participates in the creation of white battery, but is not named yet. Of course, any names are possible and it is not that important from the practical view. Let’s name it tool battery-piece or shortly TBP.

The conclusion we have here is:

а) Pieces and pawn of TBP type – can be often found in a batteries, where a fairy pieces of Нoppers type participate in a battery creation. In case of direct battery creation with a Hopper rear piece, almost always the TBP pieces are applied and in most cases they are pawns – of one or another color.

b) Usually, such kind of pieces in most of problems neither do any move, nor are captured. In the other words, they’re pretty static.

c) In which casesTBP-piece is considered as a bad piece in a problem? In case if TBP is a pawn, such a question is almost never worth. Another case, if white or black piece acts as a TBP. Then the actual question is – if this a piece, although needed in the battery construction, does it stay well on the board?

My answer is the following: if TBP is a piece, not a pawn, then it stays a little bit bad on the board in case if it acts only as a technical element of the battery. Therefore, we should try to add some additional, thematic or incidental function to our TBP! This is very important from the aestetic point of view!

For example, in our studied problem No.8 – the white Sd8 acts as TBP. But it is not a bad piece, as it has also the additional function – it guards the important square b7!

A better usage of TBP is shown in problem No.9, where pd3 acts as a TBP, and the play in 2 solutions is based exactly on the impossibility of capturing this piece!

Of course, in No.9 it is possible to remove one of the solutions and, replacing black Rook with a Bishop for example, to compose a version with just two solutions, where the blocks are done only by the white King next to the TBP-pawn. Thus, we got the scheme No.10: 1.Be5 Ke4 2.Bb2 nLOxb2-b1#; 1.Bd6 Ke3 2.Bb4 nLOxb4-b3#. By the way, here (like in No.9 as well) a Bishop-Lion also can act as a white rear piece.

No.10. Scheme

Now let’s look at some special cases, where two neutral Locusts are on the thematic battery line.

According to the battery rear piece, two neutral Locusts can create the following batteries, which deserve a special attention:

А) Direct battery with two forward pieces

B) Special battery with two forward pieces

C) Half-battery with two forward pieces

D) Special anti-batteries

Let’s look at the typical schemes:   

A) Direct battery with two forward pieces

In a scheme No.11 a thematic battery consists of 3 pieces: forward pieces –nLOf3 nLOd5, rear piece – Lion a8. Of course, it is possible here to use some other piece of Hoppers type on the square a8: LEO,VAO, Bishop Lion etc.

It is important to emphasize: it is not a half-battery, but exactly just a battery, but with two forward pieces X! Why it’s not a half-battery? Very simple – because in case of half-batteries the both forward pieces play. But here such a moment doesn’t exist – every time only one of the forward pieces plays, but at the same time the other one acts like TBP; in the second solution the pieces interchange their functions.

 

No.11. Scheme

So, let’s try to give a mate in 1 move in No.11: 1… nLOxe2-d1+?n – using the piece nLOf3 as a forward piece. This try doesn’t work, because a black answers with the move of another piece along the battery-line – 2.nLOxf5 – g5! and the battery is distructed. The analogical try is: 1…nLOxd2-d1+? but 1…nLOxf5-f6! and the battery is distructed again.

To realize H#1 is only possible blocking the squares g5/f6. Thus, a static Locust in a role of TBP-piece doesn’t have anymore an opportunity to capture the white pawn and to destruct the battery: 1.Bg5 nLOxe2-d1#; 1.Bf6 nLOnxd2-d1#.

It’s even more interesting, when during a play the both neutral Locusts are blocked, as it is shown in a problem No.12.

It’s not difficult to see, what kind of plan should be implemented here: the black Queen is sacrificed with the aim to give an opportunity for the neutral Locusts to move on vertical g. This way they give double checks with a mate.

But in the initial position it’s impossible to realize this idea. Let’s try: 1.Qf3? nLOxf3++? – now black has 2 defenses from the mate: 2.nLOcxg2-h2! and 2.nLOgxc2-b2! Analogically, the following try doesn’t lead to the goal: 1.Qf2? nLOxf2-g2++? – again black has 2 defenses from the mate: 2.nLOеxg2-h1! and 2.nLOgxe4-d5!

No.12. Petko A.Petkov

original

A plan for the solution consists of the following: to give a mate in the both solutions every time we should block two squares. These blocks by the black and white pieces are done this way: I.1.Qf3! RLh2! 2.Rb2! nLOxf3-g2#! – here h2 is blocked by white, and b2 is blocked by black; II.1.Qf2! RLh1! 2.Rd5! nLOxf2-g2#! – here h1 is blocked by white, and d5 is blocked by black.

A block of two thematic Locusts is a very nice interpretation of the theme, but it is always good if a problem has also some more interesting motives. Here they are: a) sacrifice of a black piece (it’s almost a standard motive in such a schemes); b) destuction of a black battery R/Q – the very important and interesting idea, which define the order of the black moves!

Of course, it’s possible to use some other similar batteries with the analogical location of Locusts, as the scheme No.13 shows. Here in the upper part of the position a NAO piece is used as a battery rear-piece – a very important piece in this role! In the lower part of the position a battery which can be used in help-self mates is shown.  

 

No.13. Scheme

Very often, using modifications of the standard (Queen-type) Locust – like Rook-Locust, Bishop-Locust etc. – it is possible to compose an interesting problems of different fairy genres.

A typical example is No.14: Set-play: 1…nSe5+! 2.RLOxe5-f5 Kf2! 3.Rd5 BLOxf5-g6#; Real play: 1.nSe7 nSd5! 2.RLOxd5-e5 Kg2! 3.Rc5 BLOxe5-f6#. Thematic complex here includes also non-standard motives: sacrifice of a neutral S, sacrifice of a black Rook-Locust, Bristol-theme RLO-R, black blocks.      

No.14. Petko A.Petkov

original

B) Special battery with two forward pieces

Please look at the diagram No.15 – at the first glance, a very familiar, easy position. And yet, here’s something very interesting and different to the previous examples in the section A). A stipulation #1 is realised here in a very peculiar (original) way: 1. nLOxe5-f6#! 1.nLOxd4-c3#!

No.15. Scheme

THE FIRST QUESTION: What’s this? Is this a direct battery, half-battery or anti-battery play?

My answer is: Here we have a play of a battery of a special type – with 2 forward pieces. But the piece which gives mate here, captures another forward piece and it is implemented along the battery-line with the Annihilation method! As a forward piece here we can consider a piece, which does the mating move with the capturing. In the other words, after 1.nLOxd4-c3# a piece LOe5 acts as a forward piece, but after 1.nLOxe5-f6 – LOа4 acts as a forward piece.

THE SECOND QUESTION: What practical chances this mechanism gives for composing good problems?

The answer is: The chances are simply beautiful, but it’s needed here to complicate the central motive with the other motives, among which a blockage has a central place again!

For example, in a position No.16 – white can’t give mate in 1 move with 1. nLOxe5-f6?? and 1.nLOxd4-c3?? – because these moves are impossible (illegal self-checks). It is necessary here to block the squares g3 and f2: 1.Sg3 nLOnxd4-c3#!, 1.Sf2 nLOxe5-f6#!  

No.16. Scheme

An interesting moment! Here, after 1. Sg3 the 1….nLOxg3-h2+? doesn’t work because of 2. nLOxg4-h4! Analogically: 1.Sf2 and now won’t work 1….nLOxf2-g1+? 2. nLOxb5-a5!

In the light problem No17 we can see a complex of motives: block of squares c1/d1, realized by the black Queen, Annihilation captures of pawns c6/g7, Zilahi theme, model mates. I. 1.Qxg7 2.Qg1 3.Qc1! nLOxf5-g5#; II. 1.Qxc6 2.Qh1 3.Qd1! nLOxe5-d5#. Our well-known special battery here is modified now, using the white pawn on the thematic line and a Kangaroo piece as a rear piece.

No.17. Petko A.Petkov

original

---

In the next, the 3rd part of this article, we’ll look at some other interesting batteries with Locusts!

To be continued…

---

BLOCK OF NEUTRAL BATTERY-PIECE (Part I) IGM PETKO PETKOV

---

I. INTRODUCTION

There’s one very simple, but interesting fairy idea, which might be called also the theme: block of neutral piece, which participates in a battery creation. Different variations of such batteries are possible – the neutral piece there, let’s call it “X”, can be either a forward piece, or also rear piece.

Of course, the idea can be realised in the anti-battery play as well. It should be specially mentioned, that all these possibilities are studied and used in a practise a very little yet.

But why our “Х” should be blocked during the process? The answer is simple: it should be blocked, to not allow to the side, which gets mate, to go away – to make a move with “X” to avoid the mate. Or, in the other words, the piece “X” which is blocked with the aim – to prevent its leaving of the battery-line. Also, some special situations exist, where the piece “X” has to be blocked to prevent it from the giving a check to the opposite King, when it leaves the battery-line (such moments might happen in a case, when the neutral Locust piece is used as a piece “X”).

This article is planned as a material of the numerous parts, and at the same time it is intended to the both – to the masters in composition, and also to the beginners. For these reason many of thematic effects here in the beginning are demonstrated with the simple positions – the schemes, where the only one option or solution is possible. Also, many works of the masters of Fairy genre will be presented later in the article, after the starting material will be well-learned. Of course, the theme Block of the Neutral Battery Piece can be used in all genres of composition, in other words – for all the stipulations, which determine the aim of a play: direct mates, helpmates, selfmates, and also  help-selfmates. It is possible also to realize this theme in a fairy problems with almost any of fairy conditions: Circe, Madrasi, Andernach, Take&Make etc. But in the 1st part of this material we’ll look only at the problems without additional fairy conditions which will be discussed at the very end of this cycle of articles.

Probably, the reader immediately will notice, that the theme we are reviewing, almost always are developed in conjunctions with other themes or ideas. And the richer is this synthesis, the better is the result! But at the beginning the examples will be very simple to be understandable for any reader who is familiar with the neutral pieces.

II. TYPICAL EFFECTS

So, let’s start from the simple effects of the blocks used in direct and indirect batteries. Now the series of the elementary schemes will be shown, but it is important to learn the methods of the blocks here very well as in the future it will be very much needed!

No.1. Scheme

No.1

White can’t give mate right after 1. Rf8+?? because black has a strong defense: 1….nBh2! – neutral bishop simply leaves the battery-line, and white is unable to remove this protection. But how it is possible to realise H#2 here? Of course, a simple analysis shows, that it is possible to do so in a case if black will block the square h2 for the neutral bishop. It’s easy to see how it can be done: 1. Sf1! Kb5 (this is a tempo-move of white!) 2.Sh2 Rf8#.

No.2

It’s also not very simple thing to give a mate from the battery on the vertical “a” as the rear piece of this battery is a neutral rook. For example, if we try 1.Sd8+? K~ – then the battery is absolutely useless – for the move 2…Sc3+? the neutral rook simply goes away along the 6^th horizontal, f.i. 3.nRb6! ОК. Then we have the only possibility – to block (if it is possible!) the neutral rook and to give a mate like in the example No.1.

This is how it can be done: 1. Sd4+!! Ra3!! – only this move works –the rook is prepared for the future block! 2.Sb3!! – the neutral rook is already blocked and 2…Sc3#  follows, as the rook can’t leave the battery line anymore to avoid the mate.

No.2. Scheme

Please pay your attention to this interesting idea – although, this is in the one solution only, but plays 2 “combined batteries”: the 1st one is black-neutral Sc6/nRa6 —along the 6^th horizontal, and the 2nd one is white-neutral Sa2/nRa6 – along the vertical “a”.

No.3

It is surprising, that the blocked piece can be even the neutral Queen, if it is a rear piece of the battery.

The mate is achieved after the masked battery K/Q creation in a following way: 1.nQa1 Kd5 2.nQh1 Kc6 3.g1=B+ c7# – the thematic black move here is 3.g1=B+ but the method of limiting the mobility of the neutral Q, moving it to the corner of the board, is very important for practical purposes.

No.3. Scheme

Of course, it’s possible to bloack also many fairy pieces, which participate in a batteries or anti-batteries.

No.4.

The plan of white here is to move a bishop to a2 square, and, building an anti-battery, give a mate. But the realisation of this idea is prevented by running away of the nGa5 to h5: 1. ~ Bc4 2. ~ Ba2+? , but 3. nGh5!!  That’s why the black blocks the squares in an interesting way: 1.d1=B Bc4 2.Bh5 Ba2#! – now nGh5 is not possible anymore.

No.4. Scheme

No.5.

The aim of the white here is to build the anti-battery on the vertical  “a” using nGa5 (the rear piece) and the white bishop (the forward piece). But to achieve this goal it is needed to block totally all the 3 fields which nGa5 can use to run away: c3, c5, c7. This is how it can be possible: 1.Qc3 Be5 2.Rc5 Bb8 3.Rc7 Ba7#.

No.5. Scheme

In all previous examples we were looking at the block of the rear battery-piece. But in a battery or anti-battery we can block also a forward battery-piece. The next schemes will show the typical effects of such blocks. Btw, not all the fairy pieces can be used to realize this kind of block. What you have to do here – is to choose the right fairy piece which can play the thematic role!

No.6. Scheme

No.6.

Here in the beginning we have a battery of the Rc5 (rear piece) and  nLOc7 (forward piece). But the tries to give mate in 1 one doesn’t work, f.i.: 1.nLOxb7-a7+?  but  1…nLOxc5-d4!; 1.nLOxd7-e7+?  but  1…nLOxc5-b4!  The effect of the neutral piece, which captures the another battery-piece as a defense, is shown very well here – and this is the useful effect which has to be learned!

The solution: 1.c3!  – zugzwang. Now please look at the following options: 1…d4 2n.LOxb7-a7#! — the mate is already possible as the black pawn had blocked the square d4 for the neutral locust and it can’t capture the rook! Analogically: 1…b4 2.nLOxd7-e7# —   because now the square b4 is blocked. The additional options are: 1…d6 2n.LOxd6-e5#, 1…b6 2.nLOxb6-a5#, 1…S~ 2.Bxd7#

No.7.

A try to build an anti-battery here 1.nLOхb4-b5+? – doesn’t work at the beginning, as black can answer in 2 ways: 1…nLxe2-f1+! and 1.nLOxd5-e5! The solution is clear — it is needed to block the squares f1 and e5 for the neutral Locust. This is how it can be done: 1.Bf4! Kf1! 2.Be5! nLOxb4-b5#.

No.7. Scheme

Please note the different methods of blocking — in one case the square е5 is blocked by the black, in another —  the square f1 is blocked by the white. Consequently, in some cases – especially using the neutral Locust! — the possibility of thematic block has the both sides!

So far we have discussed the schemes only, and probably some of the readers might think, that it is complicated to compose an interesting problems here. But this is not really so, as the next example shows.

No.8.

At the beginning let’s see how the play will look from the white’s move: 1…Lia3 2.Sc4! nLOxc4-c3#! The idea of the combination is clear: the white Lion blocks the neutral Locust, which after the mating move can’t give a check to the white King as the square а3 is blocked! Of course, with the sacrifice of black S, the black has created an opportunity for the neutral Locust to show it strength as an opening battery-piece of nLO/Li.

No.8. Petko Petkov

original

But here is black to move and because of zugzwang it is impossible to keep a set-play. So, the new play is needed! It is possible, realizing the analogical thematic: I. 1.Sd3 Lia2 2.Sc5+ nLOxc5-c4#; II. 1.Sd1 Lia4 2.Sc3 nLOxc3-c2#. Three-phase play between the Lion and the neutral Locust here has a form of duel, and an important additional motive: the black S is three times sacrificed on different squares!

---

In the next part we’ll look at more complicated examples with the battery-pieces like Chameleons, Chinese pieces etc.

To be continued…

---