|
|
Original Problems (page 49)Original fairy problems published during 2012 will participate in the informal tourney JF-2012. The site is mostly about fairies, but h# and s# are also welcomed for publication! Please send your problems to my e-mail: julia@juliasfairies.com Go to →List of Problems; →Page 48 ; →Page 50 |
The 1st problem of the next hundred is welcomed!
No.101 – ser-#6 by Peter Harris – Aristocrat miniature with series direct play and difficult solutions. (JV)
My problem No.100 is between 2 problems by Peter – No.99 and No.101! – Can I make a wish? 🙂
Definitions:
Ultra-Patrol Chess – A piece can move, capture or give check only if it is observed by a piece of its own side.
Sentinels: when a piece (Ks included but not pawns) moves, a pawn of the same colour appears on the vacated square unless that square is on the first or eighth ranks or there are 8 pawns of that colour on the board already.
You can сlick on “Solutions” to show or hide the solutions!
|
No.101 Peter Harris
South Africa
original-18.08.2012
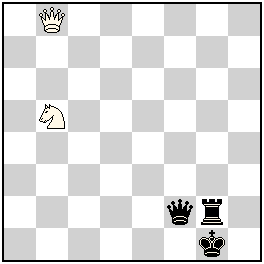 ser-#6 b) Sb5→b6 (2+3)
Sentinels
Ultra-Patrol
Solutions: (click to show/hide)
|
The diagrams are made on WinChloe and its Echecs font is used for Logo design



Dear Peter,
Happy Birthday to You!!
Your problems are very complicated and your activity is amazing! Thank you for it!!
Julia.
Happy birthday Peter !!
I have a couple of questions.
What exactly is the idea of the problem?
Why bQf2 instead of bRf2?
EXACTLY it is that in one solution f2g2 are captured while in the other they are not.
There is a Qf2 and not a R because that is what I preferred.
There are some who enjoy solving chess problems and others who do not. Some solvers look upon a problem primarily as a duel between them and the composer. They enjoy the challenge. They relish the play and discovering the unexpected. If they succeed they feel triumphant. If they fail, they accord the composer his due – but promise that the next time they meet things will be different. On the other hand there are those who when they see a problem immediately click on Solutions. They give the problem an exhaustive technical examination. They have a large bagful of terminology. They are able to give name to a hundred themes and mechanisms. They must find a reason for the problem. In the order of things, economy and compatibility take precedence over originality and interest. This distinction between solvers and non-solvers is also to be found in types of problems and their composers. [It will also be mirrored in the types of comments made]. If both types of problems can have beauty, I think there is more life in the one than in the other.
Peter, I think I understand your point. Let me state mine.
As someone who is more composer than solver, I prefer composing to solving. However, I solve problems time to time, once upon a time I have regularly solved in Springaren, Phenix, Sachove umeni and less regularly feenschach. Both orthodox and fairy problems. I have never been excellent solver (I hold only about 2200 solving rating) and only my vast fairy composing experience can be probably blamed for my win in fairy solving competition at WCCC at Crete 2010.
I am writing all this just to state the background for my view. I.e. I hope my words are not just words by nobody, somebody with no experience, just theorizing guy.
Even as a solver, I enjoy finding composers idea related to beauty, not just difficulty of the problem. I can enjoy AUW, Cyclone, strategic, formal theme, even the most weird ideas without own names, but there should be one. Problem, that is just difficult, but nothing else, does not excite me.
And the issue with a part of current fairy production is the following. It is just difficult with little valuable content. It repels significant share of solvers because their solving effort is not rewarded by feeling of beauty after finding the solution. Only small fraction of solvers, these with desire to solve no matter what the content is, are satisfied by cracking the hard problems.
Of course, such difficult problems have the right of existence, after all they deliver at least to a part of solving public. Even if they would not deliver to anyone, such problems can exist. The point is in the balance – too many such problems compared to their attractiveness.
Any other views?