THE AWARD of Christmas Blitz JF-2014, Section B
In this section participated 27 problems and most of them show very original and interesting ideas.
The following problems were not included in the award due to non-compliance with the requirements of the tournament: No.13 Peter Harris and No.29 Peter Harris – both problems have a stipulation Ser-HS#(=) in “n” moves that is not allowed by the rules of this TT. The very interesting ser-h#13, No.64 by Oliver Sick was also not included because the maximum permitted number of moves here is 8.
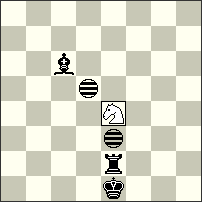
| No.32 Peter Harris South Africa Christmas Blitz JF-2014 Section B 1st-2nd Prize Dedicated to Julia Vysotska |
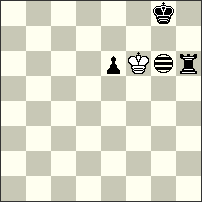
No.75 Kostas Prentos USA Christmas Blitz JF-2014 Section B 1st-2nd Prize |
No.77 Kostas Prentos USA Christmas Blitz JF-2014 Section B 3rd Prize |
 |
 |
 |
| hs#4 2 solutions (1+3+2i) Imitators: d5, e3 Maximummer Royal Se4 |
hs#3.5 2 solutions (1+3+1i) Imitator g6 |
hs#4 b) -Pf7 (4+1+1i) Imitator e5 |
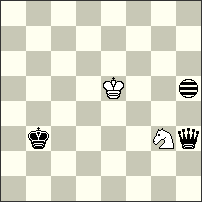
1st-2nd Prize – No.32 Peter Harris. A very elegant Aristocrat constructed with 4 pieces and 2 Imitators! The main thematic idea here is the interchange of functions between black Rook and Bishop – their moves are guided by two black Imitators! The mates follow after play of a very strange “fairy battery” that has a Rook (or Bishop) as a “rear piece” and three pieces(!!) as “forward pieces” – the other black piece and both Imitators! Noteworthy is that in the two phases the Royal white Knight makes 8 different moves! I. 1.rSe4-g5[If6,g4] Bc6-a8[Id8,e6] 2.rSg5-f3[Ic6,d4] + Ba8-c6[Ie4,f2] 3.rSf3-h4[Ig5,h3] Re2-a2[Ic5,d3] 4.rSh4-g2[Ib3,c1] Ra2-a6[Ib7,c5] #; II. 1.rSe4-f6[Ie7,f5] Re2-a2[Ia7,b5] 2.rSf6-g4[Ib5,c3] Ra2-f2[Ig5,h3] 3.rSg4-e5[Ie6,f4] Bc6-a4[Ic4,d2] 4.rSe5-f7[Id6,e4] Ba4-d1[Ig3,h1] #
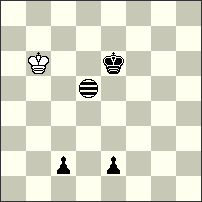
1st-2nd Prize – No.75 Kostas Prentos. Here we see white “Rex solus” and the achieving of the goal in this Tanagra position seems improbable. But there follows a marvellous series of great manoeuvres of White and Black, which leads again to zugzwang and mate to the white King!! Two unexpected echo-finales are another great ornament of this problem with a charming dance of the thematic pieces Kf6, Kg8,Rh6, Ig6! I. 1…Rh6-h7[Ig7] 2.Kf6-g5[Ih6] Rh7-f7[If6] 3.Kg5-h6[Ig7] Rf7-g7[Ih7] 4.Kh6-h7[Ih8] Kg8-f8[Ig8] #; II. 1…Kg8-h7[Ih5] + 2.Kf6-e7[Ig6] Rh6-g6[If6] 3.Ke7-f8[Ig7] Rg6-g7[Ig8] 4.Kf8-g8[Ih8] Kh7-h6[Ih7] #
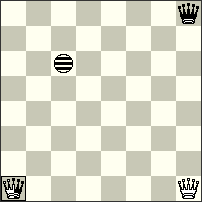
3rd Prize – No.77 Kostas Prentos. It is clear in this black “Rex solus” problem that the black King must give mate after cunning manoeuvres. Three black Imitators help both sides to achieve the goal in the first phase! In the twin – after the very surprising elimination of the wPf7 – a similar plan is implemented, but this time in a completely different manner and with only two Imitators! A very unusual content excellently demonstrates the Imitator’s power to achieve zugzwang before Black’s mating move! a) 1.f7-f8[Ie6]=I Kc6-d6[If6,g8] 2.Re8-e5[If3,g5] Kd6-d7[If4,g6] 3.h7-h8[If5,g7]=I Kd7-c6[Ie4,f6,g7] 4.Re5-f5[If4,g6,h7] Kc6-b7[Ie5,f7,g8] #; b) 1.Ka7-a8[Ie6] Kc6-d6[If6] 2.h7-h8[If7]=I Kd6-c6[Ie7,g8] 3.Re8-e2[Ie1,g2] Kc6-b6[Id1,f2] 4.Re2-c2[Ib1,d2] Kb6-a7[Ia2,c3] #
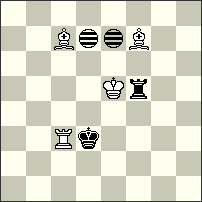
| No.11 Peter Harris South Africa Christmas Blitz JF-2014 Section B 4th Prize |
No.86 Eric Huber & Vlaicu Crișan Romania Christmas Blitz JF-2014 Section B 5th Prize |
 |
 |
| hs#4 2 solutions (4+2+2i) Imitators: d7, e7 |
ser-h#5 b) Kg6→f8 (1+1+2+1i) Imitator e2 Chameleon Chess, NoIProm |
4th Prize – No.11 Peter Harris. Another Aristocrat where actively play all white and black pieces! The role of both Imitators is very interesting! Of course, there is no complete thematic identity between the two solutions but I do not think that this is a minus of the problem. Therefore, the problem belongs to the so-called “ANI-TYPE”) but I think this is the “Formula of the future”! Many originals in this competition are composed in ANI-style! I. 1.Bc7-b6[Ic6,d6] + Rf5-f4[Ic5,d5] 2.Bf7-g6[Id4,e4] Rf4-e4[Ic4,d4] + 3.Rc3-c7[Ic8,d8] Re4-d4[Ib8,c8] 4.Bg6-f5[Ia7,b7] Rd4-d5[Ia8,b8] #; II. 1.Bc7-d6[Ie6,f6] + Rf5-h5[Ig6,h6] 2.Bf7-e6[If5,g5] Rh5-h2[If2,g2] 3.Rc3-a3[Id2,e2] Rh2-f2[Ib2,c2] 4.Be6-d5[Ia1,b1] + Kd3-d4[Ia2,b2] #
5th Prize – No. 86 Eric Huber & Vlaicu Crișan. In a Tanagra form – neutral Chameleon AUW with difficult solutions though the length of the problem is “only” 5 series-moves. I think that in such tasks it is particularly valuable to achieve the use of all pieces in the mating finales. a) 1.nPa2-a1[Ie1]=nS 2.nSa1-b3[If3]=nB 3.nPf2-f1[If2]=nQ 4.nQf1-b1[Ib2]=nS 5.nBb3-g8[Ig7]=nR Kd7-e6[Ih6] #; b) 1.nPf2-f1[Ie1]=nB 2.nBf1-e2[Id2]=nR 3.nPa2-a1[Id1]=nR 4.nRa1-b1[Ie1]=nQ 5.Kf8-e8[Id1] nQb1-f1[Ih1]=nS #
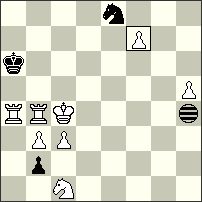
| No. 80 René J. Millour France Christmas Blitz JF-2014 Section B Special Prize |
No.50 Cornel Pacurar Canada Christmas Blitz JF-2014 Section B Special Prize |
 |
 |
| hs#2 4 solutions (8+3+1i) Imitator h4 Chameleon Pf7 |
pser-h#6 2 solutions (2+2+1i) Imitator e2 |
Special Prize – No. 80 René J. Millour. The Babson theme is of course an eternal theme in chess composition – it is well known also that this theme is a lovely “arena” of R.J.Millour. To compose a Babson task in 2 moves in Meredith form is rather difficult, of course. In this respect, the content here also includes some false attempts to promote Pc2 into other pieces. I appreciate and welcome the efforts of the author! But here the captures of the technical Se8/Sc1 spoil to some extent the aesthetic perception. Unfortunately, such minuses are inevitable in almost all Babson tasks. I. 1.cPf7*e8[Ig5]=cQ + b2*c1[Ih4]=Q=c 2.cQe8-c6[If2]=cS + cQc1-e3[Ih4]=cS #; II. 1.cPf7*e8[Ig5]=cS + b2*c1[Ih4]=S=c 2.cSe8-c7[If3]=cB + cSc1-e2[Ih4]=cB #; III. 1.cPf7*e8[Ig5]=cR + b2*c1[Ih4]=R=c 2.cRe8-b8[Ie4]=cQ + cRc1-f1[Ih4]=cQ #; IV. 1.cPf7*e8[Ig5]=cB + b2*c1[Ih4]=B=c 2.cBe8-b5[Ie1]=cR + cBc1-f4[Ih4]=cR #
Special Prize – No.50 Cornel Pacurar. Another excellent Tanagra with a very strange idea! Optically, the mate pictures are almost identical in both phases, but in fact there are two significant differences between the play in the first solution (block on e3 with a Knight!) and in the second solution (block on e3 with a Queen!). At the same time, the w.King realises two quite different paths to square “f2″! I. 1.c2-c1[Ie1]=S + Kd3-e3[If1] 2.Sc1-d3[Ig3] 3.Kg4-g3[Ig2] 4.Kg3-f2[If1] + Ke3-f4[Ig2] 5.Kf2-e2[If2] + Kf4-g3[Ig1] 6.Ke2-e3[Ig2] Kg3-f2[If1] #; II. 1.c2-c1[Ie1]=Q 2.Qc1-b1[Id1] + Be5-d6[Ic2] 3.Kg4-f5[Ib3] + Kd3-e2[Ic2] 4.Qb1-d3[Ie4] + Ke2-f2[If4] 5.Kf5-e4[Ie3] 6.Ke4-e3[Ie2] + Bd6-e5[If1] #
| No. 85 Eric Huber & Vlaicu Crișan Romania Christmas Blitz JF-2014 Section B 1st Hon.men. |
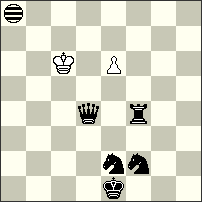
No.90 Diyan Kostadinov Bulgaria Christmas Blitz JF-2014 Section B 2nd Hon.men. |
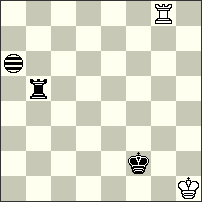
No.30 Peter Harris South Africa Christmas Blitz JF-2014 Section B 3rd Hon.men. |
 |
 |
 |
| pser-h#5 2 solutions (2+2+1i) Imitator h5 |
ser-h=5 (1+3+1i) b) Id5→b4, c) Kb6→h6 Imitator d5 |
hs#4 b) hs=4 (1+1+1+1i) Imitator c6 Royal Qa1 |
1st Honourable Mention – No. 85 Eric Huber & Vlaicu Crișan. In the both phases the Imitator occupies two most distant squares of the board – the corners a1 and h8! This is a very pleasant surprise – not only for the solvers! However, it seems to me that in the Pser-h# a large number of checks to the w.King is not particularly valuable. In such cases, the solutions become quite forced in character… I. 1.Qh3-f5[If7] + Ke5-d4[Ie6] 2.Qf5-f4[Ie5] + Sg3-e4[Ic6] 3.Kb3-c2[Id5] 4.Qf4-e3[Ic4] + Se4-c3[Ia3] 5.Kc2-d2[Ib3] + Sc3-b1[Ia1] #; II. 1.Qh3-h5[Ih7] + Sg3-f1[Ig5] 2.Kb3-b2[Ig4] + Ke5-e6[Ig5] 3.Qh5-f5[Ie5] + Ke6-f7[If6] 4.Kb2-c2[Ig6] + Sf1-e3[If8] + 5.Kc2-d1[Ig7] Kf7-g8[Ih8] #
2nd Honourable Mention – No.90 Diyan Kostadinov. The author wrote: “Reciprocal AB-BA 1st and 3rd moves between twins a) and b). Reciprocal Imitator/Bishop promotions between twins a) and c).” OK, it is a non-standard concept in optimal construction, but here a full cyclic harmony doesn’t exist between the three solutions. a) 1.e2-e1[Id4]=I 2.Ke6-d7[Ic5,d2] 3.c2-c1[Ic4,d1]=B 4.Kd7-c8[Ib5,c2] 5.Kc8-b8[Ia5,b2] Kb6-b5[Ia4,b1] =; b) 1.c2-c1[Ib3]=B 2.Bc1-d2[Ic4] 3.e2-e1[Ic3]=I 4.Bd2-f4[Ie5,g3] 5.Ke6-e5[Ie4,g2] Kb6-c5[If3,h1] =; c) 1.e2-e1[Id4]=B 2.Be1-h4[Ig7] 3.c2-c1[Ig6]=I 4.Bh4-f6[Ie8,a3] 5.Ke6-f5[If7,b2] Kh6-g5[Ie6,a1] =
3rd Honourable Mention – No.30 Peter Harris. An interesting Four-man problem that demonstrates a nice duel between the rnQa1 and bQh8. The twin is also non-standard. But in my opinion the role of w.Qh1 that realizes a “sacrificial introduction” is rather modest and artificial. a) 1.Qh1-h3[Ic8] Qh8*h3[Ic3] 2.nrQa1-c3[Ie5] Qh3-e6[Ib8] 3.nrQc3-g3[If8] Qe6-a2[Ib4] 4.nrQg3-g1[Ib2] Qa2-g8[Ih8] #; b) 1.Qh1-f1[Ia6] nrQa1*f1[If6] 2.nrQf1-e2[Ie7] Qh8-d4[Ia3] 3.nrQe2-h5[Id6] Qd4-g1[Ig3] 4.nrQh5-h4[Ig2] Qg1-a7[Ia8] =
| No.20 Kenneth Solja Finland Christmas Blitz JF-2014 Section B 4th Hon.men. |
No.6 Stephan Dietrich Germany Christmas Blitz JF-2014 Section B Special Hon.men. |
 |
 |
| ser-h=6 b) Id1->g1 (2+8+2i) Imitators: a2, d1 |
hs#3 2 solutions (2+11+2i) Imitators: c2, g2 |
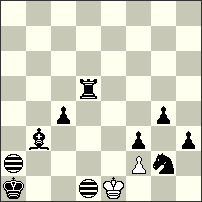
4th Honourable Mention – No. 20 Kenneth Solja. Nice stalemate finales, where the leading role is played by the white King. In my opinion it’s a very difficult problem for solvers! a) 1.Sg2-h4[Ib4,e3] 2.Ka1-b2[Ic5,f4] 3.Kb2-c1[Id4,g3] 4.Sh4-g2[Ic2,f1] 5.Rd5-f5[Ie2,h1] 6.Kc1-c2[Ie3,h2] Ke1-d2[Id4,g3] =; b) 1.Rd5-e5[Ib2,h1] 2.Sg2-f4[Ia4,g3] 3.Re5-e3[Ia2,g1] 4.Ka1-a2[Ia3,g2] 5.Ka2-a3[Ia4,g3] 6.Sf4-g2[Ib2,h1] Ke1-d1[Ia2,g1] =
Special Honourable Mention – No.6 Stephan Dietrich. A nice symbolic problem that beautifully paints a Christmas-tree! I. 1.Ke1-f1[Id2,h2] c3-c2[Id1,h1] 2.e7-e8[Id2,h2]=R Ke3-d2[Ic1,g1] 3.Kf1-e1[Ib1,f1] Sd3-c5[Ia3,e3] #; II. 1.Ke1-f1[Id2,h2] f3-f2[Id1,h1] 2.e7-e8[Id2,h2]=I Ke3-d2[Ic1,g1,d7] 3.Kf1-g1[Id1,h1,e7] Qe5-d6[Ic2,g2,d8] #
Commendations (without order and comments):
| No. 9 Karol Mlynka Slovakia Christmas Blitz JF-2014 Section B Commendation |
No.60 Alberto Armeni Italy Christmas Blitz JF-2014 Section B Commendation |
No.12 Peter Harris South Africa Christmas Blitz JF-2014 Section B Commendation |
 |
 |
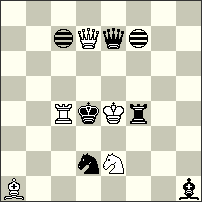 |
| pser-h#4 (2+2+1i) b) Rg8→g6, c) Rg8→e5, d) Kf2→b3, e) Kf2→a8 Imitator a6 |
ser-h=4 (2+5+1i) b) Ke1→f1, c) Ia8→d8, d) Ia8→f8, e) Ia8→e7, f) Se2→e3 Imitator a8 Chameleon Chess |
hs=4 (5+5+2i) b) Chameleon Chess Imitators: c7, f7 |
Commendation – No. 9 Karol Mlynka. a) 1.Kg3[Ib7] 2.Rh5[Ih7]+ Kg1[Ig7] 3.Kh2[Ih6]+ Kf1[Ig6] 4.Rh6[Ig7] Rg2[Ig1]#; b) 1.Rb4[Ia5] 2.Rh4[Ig5]+ Kg2[If6]+ 3.Ke3[Ie7] 4.Rf4[Ic7] Re6[Ia7]#; c) 1.Rb7[Ia8] 2.Rg7[If8] 3.Kg2[Ig8]+ Rf5[Ih8] 4.Kg1[Ih7] Rf4[Ih6]#; d) 1.Rh5[Ig6]+ Kg2[If7] 2.Rh2[If4]+ Kf3[Ie5] 3.Rh3[Ie6]+ Ke4[Id7] 4.Kc4[Ie8] Rc8[Ia8]#; e) 1.Kb8[Ib6] 2.Rb1[Ib2]+ Rh8[Ic2] 3.Ka8[Ib2]+ Kg2[Ia3] 4.Rh1[Ig3] K*h1[Ih2]#
Commendation – No.60 Alberto Armeni. a) 1.Se2-g1[Ic7]=B 2.Sf2-d1[Ia6]=B 3.Rf4-f1[Ia3]=Q 4.Qd4-h8[Ie7]=S Kc6-d7[If8] =; b) 1.Rf4-g4[Ib8]=Q 2.Qg4-g1[Ib5]=S 3.Sf2-h3[Id6]=B 4.Qd4-b6[Ib8]=S Kc6*b6[Ia8] =; c) 1.Rf4-f3[Id7]=Q 2.Sf2-d3[Ib8]=B 3.Qf3-f1[Ib6]=S 4.Qd4-c5[Ia7]=S Kc6-c7[Ia8] =; d) 1.Sf2-d1[Id7]=B 2.Rf4-f5[Id8]=Q 3.Qd4-g1[Ig5]=S 4.Qf5-f7[Ig7]=S e6*f7[Ih8] =; e) 1.Ke1-f1[If7] 2.Qd4-d3[If6]=S 3.Sd3-e1[Ig4]=B 4.Rf4-f7[Ig7]=Q e6*f7[Ih8] =; f) 1.Rf4-h4[Ic8]=Q 2.Se3-f1[Id6]=B 3.Qd4-a1[Ia3]=S 4.Qh4-h8[Ia7]=S Kc6-c7[Ia8] =
Commendation – No.12 Peter Harris. a) 1.Ke4-f5[Id8,g8] + Rf4-g4[Ie8,h8] 2.Qd7-c7[Id8,g8] + Rg4-g3[Id7,g7] 3.Qc7-d6[Ie6,h6] + Rg3-g1[Ie4,h4] 4.Qd6-c5[Id3,g3] + Kd4-e4[Ie3,h3] =; b) 1.Ke4-d5[Ib8,e8] + Kd4-e3[Ic7,f7] 2.Rc4-c5[Ic8,f8]=Q Qe7*c5[Ia6,d6]=S 3.Kd5-e5[Ib6,e6] Sd2-c4[Ia8,d8]=B 4.Qd7-d1[Ia2,d2]=S + Rf4-f5[Ia3,d3]=Q =


When I am browsing solutions of problems with imitators, I always wonder whether there is at least one soul who is willing to try solving such problems. Do you know someone? I do not.