| No.405, 406 Peter Harris (South Africa) |
Original Problems, Julia’s Fairies – 2013 (III): September- December →Previous ; →Next ; →List 2013(III) Please send your original fairy problems to: julia@juliasfairies.com |
No.405 by Peter Harris – A nice specific battery-play! Author writes: “The problem I am sending now could not be made without using the 3 conditions I have used.” (JV)
No.406 by Peter Harris – Two pieces are playing with a combination of six(!!) fairy conditions! I’d like to quote the author here again: “Is there a curious soul who, midst all the conditions, will enjoy finding the serial moves? But the most important question of all is: Is there a real Fairy Land somewhere?” (JV)
Definitions:
Transmuted Kings: When they are threatened, the Kings move only like the threatening unit(s).
Einstein chess: all units (Ks excluded) change their type when they move, according to a precise pattern. For non-capture moves: Q>R, R>B, B>S, S>P, P remains P. For capture-moves: R>Q, B>R, S>B, P>S, Q remains Q. Pawns do not promote. A Pawn on its eighth rank is dead. Pawns can move from their first rank. Their first move can be three squares and they can capture pieces on their second rank.
Isardam – any move, including capture of the King, is Isardam illegal if a Madrasi-type paralysis would result from it.
Madrasi – like units other than Kings are paralysed when they attack each other. Paralyzed units can not move, capture or check, their only power being that of causing paralysis.
Patrol Chess: A piece can capture or give check only if it is observed by a piece of its own side.
Maximummer – Black must play the geometrically longest move or may choose from among longest moves of equal length, distances being measured from the center of each square. Diagonal and oblique distances are measured from the orthogonal coordinates by using Pythagora’s theorem (take the square root of the sum of the squares of the orthogonal distances). All other orthodox chess rules apply.
White Maximummer – Only White must play the geometrically longest moves, Black plays orthodoxal.
Sentinels: when a piece (Ks included but not pawns) moves, a pawn of the same colour appears on the vacated square unless that square is on the first or eighth ranks or there are 8 pawns of that colour on the board already.
Super-Circe – When captured, a piece is reborn on any free field on the chess board without causing self-check or selfmate. Possible is also removal of captured piece from the board. The Pawns (white, black, neutrals, half- neutrals) can be reborn on the first or eight row also. When reborn on the first row (for Black) or on the eight row (for White) the promotion is obligatory. When reborn on the first row (for White) or on the eight row (for Black) the Pawns are immovable.
Chameleon Chess: All pieces on the board which are displayed as orthodox Q, R, B, S, are Chameleons. A Pawn can promote only in Chameleon-pieces.
Chameleon: On completing a move, a Chameleon (from classical standard type) changes into another piece, in the sequence Q-S-B-R-Q… Promotion may be to a chameleon at any stage in the cycle.
Anti-Andernach – A piece (excluding King) changes its color after any non-capturing move. After capture, the piece retains its color. Rooks on a1, h1, a8 and h8 can be used for castling, provided the usual other rules for that move are satisfied. After castling, Rooks do not change color, If White makes a non-capturing move with neutral or halfneutral piece, that piece becomes black and vice versa.
|
No.405 Peter Harris
South Africa
original – 28.10.2013
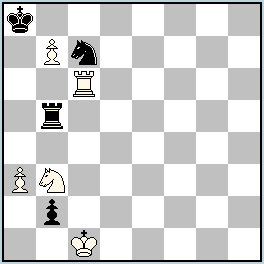 hs#3 b) wPa3→f4 (5+4)
Transmuted Kings Einstein Chess Isardam Solutions: (click to show/hide)
|
No.406 Peter Harris
South Africa
original – 28.10.2013
 ser-h#5 (1+1)
Patrol Chess White Maximummer Sentinels Super-Circe Chameleon Chess Anti-Andernach Solutions: (click to show/hide)
|



No. 406. The solving process.
One of the conditions is PatrolChess – so a White piece has to be created.
This will be done using the Sentinelles and AntiAndernach conditions.
Considering:
that the K has to be confined and mated in only 5 moves
the position of the wB
the ChameleonChess condition
the following two things are likely
the K will be at a1
the White piece created will be a R [to become a Q on mating].
So after 3 of the 5 serial moves the position is likely to be [as per the problem]:
bKa1, bPa2, wRb1.
[A question arises is: what else could the first 3 moves possibly be?]
Black now has only 2 moves left.
It is at this juncture [bearing in mind the Whitemaxi and PatrolChess conditions] it could be guessed that the mating position is likely to be [as per the problem] namely:
W: Qg1 Bd4 B: Ka1 S/Ba2
The 4th [second last move] will be bPa2*wR. The 5th and last move will be to attend to the task of blocking a2.
The only way a Black piece can arrive on a2 is for it to be sent there by White using Supercirce – so Black has to arrange that a Black piece is captured by White when mating.
Black cannot simply move to the envisaged mating square by 5. Black piece b1 > White mating square [g1] because it will have changed colour. So to retain blackness Black when moving to the White mating square must capture i.e. 5. Black piece b1*wR. This explains the placement of the wR on g1 [with the move 4. bPa2*wR].
With 5. Black piece*wRg1 the R rebirth square has to provide for the Whitemaxi condition and for the necessity [because of PatrolChess] to be observed by the wBd4 to enable White to make a capture [on g1] – so rebirth on g8 [instead of g7] will not do.
Finally the Black piece made with 4. a2*wRb1 cannot be a R; because while a bR could capture wRg1, it would become a Q and when this bQ was reborn on a2 Black could [despite the double-check] avoid mate by moving bQ-f2 = wS. The S would disempower both checking pieces. So the Black piece made upon 4, a2*wR has to be a Q.
Black’s 4th and 5th moves are not so difficult to find.
It could be said that the solution as a whole plays itself – there being no plausible alternatives. In other words solving is not so difficult.
{For those interested: I conceived this idea in my head without involving a computer].
Multi-condition problems are criticised on two grounds. Firstly that all the conditions are not used enough in the play and secondly that they are too difficult to solve. Both criticisms can be justified. However (i) regarding under-usage: the question of degree arises and (ii) regarding difficulty: often solving is not as difficult as made out – if solvers put their minds to it – and do not, as a reflex action, run away screaming.
There is the simple fact that certain ideas can be shown only with multi-conditions. I would like to repeat this sentence.
A partial explanation of solvers attitude to multi-condition problems is that to solve them can require creativity – which is not their forte – as opposed to analysis.
The Fairy world will be the loser if it does not embrace multi-condition problems.