|
|
Original Problems, Julia’s Fairies – 2014 (I): January – April →Previous ; →Next ; →List 2014(I) Please send your original fairy problems to: julia@juliasfairies.com |
No.487 by S. K. Balasubramanian – An interestin
Definitions:
Locust(L): Moves along Queen lines only by capturing an enemy unit, arriving on the square immediately beyond that unit, which must be vacant.
Take & Make: Having captured, a unit must immediately, as part of its move, play a non-capturing move in imitation of the captured unit from the capture-square. If no such move is available, the capture is illegal. Promotion by capture occurs only when a pawn arrives on the promotion rank as the result of a take&make move. Checks are as in normal chess: after the notional capture of the checked K, the checking unit does not move away from the King’s square.
|
No.487 S. K. Balasubramanian
India
original-17.01.2014
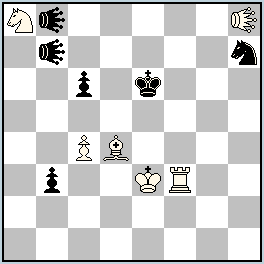 hs#3,5 2 solutions (6+6) hs#3,5 2 solutions (6+6)Take & Make Locusts: b7, b8, h8 Solutions: (click to show/hide)
|


 No.487
No.487 
Locusts can’t be captured in Take&Make, because they can’t make non-capturing moves. It is hard for a king to escape check from an adjacent locust, but it can be done by blocking the locust’s arrival square. In each solution locusts from each side set up matching attacks on the opposing king, with the mating moves being a special kind of cross-check in which a black locust removes the white blocking piece and becomes a blocking piece itself. The matching sacrifices of the bS on f6/f8 and wS on b6/c7 are very pleasing. Another exceptionally good problem from this composer!
Dear Geoff,
Thanks for your pleasing comments.
Beautifully matched solutions with typical Locust blocking/unblocking effects. Great problem!
SBK..? 🙂
Sorry, my mistake in initials.. SKB of course! I’ve corrected the name of the page now!
Excellent problem with rich thematic content!
Thanks Seetharaman & Diyan.
A beautiful problem by Indian maestro!
I’ve spend a long time, trying to improve some things in the construction, but couldn’t succeed until now.
It turns out, that it is quite not easy and maybe impossible at all.
To my opinion, this is one of the best professor’s problems!