Preliminary Award JF-2013-I

JULIA’S FAIRIES 2013/I

Preliminary AWARD

(becoming final after 1 month, 17.07.2013)

Dear Friends!

When I agreed to judge this competition, I never thought that so many problems would participate! For the 4 months of the competition there were 94 problems (without versions) from 40 authors of 20 countries, while other competitions would not receive half this amount during a whole year! This is a great success for the Julia’s Fairies website.

But that is not all. The site is not only a place where many interesting and original problems appear, it also creates a society of enthusiasts of fairy chess who show their compositions and share their experiences, leading to creative discussions. And most importantly – they address each other politely, with great understanding and admiration of all this wonderful world of free creativity has to offer. I had the feeling that it was not a competition, but a creative laboratory, working for the glory of fairy chess composition. Therefore it was very difficult to judge such a competition from the outside. But finally, under the site’s influence, I felt part of this society and, despite minor errors in the content of individual problems, felt the same delight as the authors had while composing these problems.

The average level of the participating problems was quite high and I did not find one weak composition. Among the many problems with rich and interesting content there were nine which especially interested me, and which I’ve decided to award with prizes. But almost all the others were different just in some details, and these details determined their evaluation. In addition to the nine prizes I’ve decided to award ten honorable mentions and also ten commendations. 

This is my AWARD

No.288 Juraj Lörinc Slovakia Julia’sFairies – 2013/I 1st Prize   #2                                              (11+12) Anti-Circe type Cheylan Camel-Riders: d2, e2 Rook-Kangaroo-Lions: g2, h8, c8

Solutions: key threat 1…hxg1Q (Qd8) a 1…hxg1S (Sb8) b 1…hxg1B (Bf8) c 1…RKLc4 d refutation 1.f8CR? 2.RKLa8# 2.CRxb3 (CRb8)# A 2.CRxd5 (CRd8)# B – 2.CRxc7 (CRc8)# X 1…Bg8! 1.b8CR? 2.RKLa8# 2.CRxf5 (CRf8)# C – 2.CRxd5 (CRd8)# B 2.CRbxc5 (CRc8)# Y 1…Ra1! 1.d8CR! 2.RKLa8# – 2.CRxf5 (CRf8)# C 2.CRxb3 (CRb8)# A 2.CR8xc5 (CRc8)# Z

1st Prize: No. 288, Juraj Lörinc

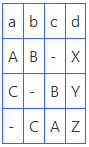A problem with a very rich strategic and new-strategic content. The center of gravity of the whole problem lies in the effort to allow (by White) or reject (by Black) the move 2.RKLa8#. This move is possible when there are two hurdles on the eighth rank and impossible when there are either one or three hurdles. So White tries to provide the second hurdle with a pawn promotion on f8, b8 or d8. It seems that white pawns can promote into any piece, but it is not so! Pawns in all phases always promote into Camel-Riders, for reasons that only become clear in the conclusion. Black defends with promotions into Q, B and S with the move 1…hxg1, resulting in the rebirth of these pieces on the 8th rank. But the rebirth-squares for these pieces are the same squares where the white pawns were promoted on the 1st move. So, Black can promote only into those pieces whose rebirth squares are not occupied.

And now for the second act. The pawn b2 is pinned, but after any check from the Rook-Kangaroo-Lion on g2 (after a move by the Camel-Rider e2) it is unpinned and the check can be avoided by playing 1…bxc1. At the same time this pawn should promote only into those pieces having the same rebirth-squares f8, b8 or d8! But if these three squares are already occupied then promotion becomes impossible and the pawn remains immobile. This is exactly what is used by White on the final move. White opens the battery with a move by the Camel-Rider e2, which, after capturing a pawn on one of the files b, d, or f, is reborn on the last free square on the 8th rank and mates the black King. Thus, a great strategic battle for seizure of the eighth rank finally ends with a triumphant shot from the battery on the second rank. This exciting carousel cyclically alternates in two variations in all three phases!

But there is a 3rd act! Black can also defend my moving its hurdle on the 8th rank, namely the Rook-Kangaroo-Lion, which can move to c4. But now it becomes clear why White promoted the pawns into Camel-Riders on the first move! This is the only piece capable of capturing on the “c” file to be reborn on c8, which is the square left by the black piece, and to mate from there. Thus a three-phase change is added to the carousel change, and the new-strategic content expands from Z-32-33 to Z-33-46.

The refutations are very good. After 1.f8 Black uses the opening of a line to his own Bishop allowing an interference on g8, while after 1.b8 he uses block of b8 and defence by unblock of b1 (the Camel-Rider is unable to capture on b1 because of block of its rebirth-square b8).
Without a doubt, the best problem of the tournament.

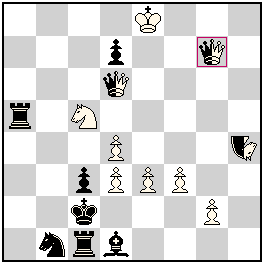
No.225 Petko A. Petkov Bulgaria Julia’sFairies – 2013/I 2nd-3rd Prize ex aequo h#2                b) Pf2→f3         (3+7+3) c) Pf2→f4 NAO c8; PAO c4; VAO a8

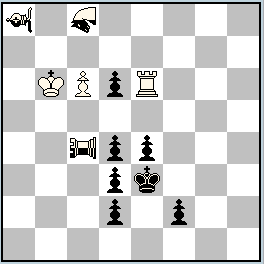
No.270 Julia Vysotska & Michel Caillaud Latvia / France Julia’sFairies – 2013/I Dedicated to Petko A. Petkov in occasion of his birthday! 2nd-3rd Prize ex aequo h#2,5                                       (7+7+4) b) Neutral Chameleon Rg7 Neutral Nightrider h4 Neutral Chameleon Qg7

2nd-3rd Prize: No. 225, Petko A. Petkov and No. 270, Julia Vysotska & Michel Caillaud

225: a) 1.nNAg6! nPAxe4 2.nNc4!! nPAxc4#; b) 1.nVAb7! nNAxe4 2.nVAc8!! nNAxc8#; c) 1.nPAa4! nVAxe4 2.nPAa8!! nVAxa8#

Perfect cooperation between three Chinese neutral pieces with a black pawn at the control of squares f2, f3 and f4, and the capture of the pawn e4 resulting in the creation of three different batteries. When a black pawn is on the square f2, this square does not need be controlled by the neutral Nao c8, which is free to go in two moves to the square c4, where there stands a neutral Pao. The neutral Pao on the first move vacates the square c4 and captures on e4, preparing a Rook-battery for the mate. On the second move the battery will fire, the neutral Pao returning to the square c4. But that square is already occupied by the neutral Nao, which arrived there on the previous move, and without this move the return would be impossible (the neutral Pao e4 can return to the square c4 only with a capturing move, which the neutral Nao’s move to c4 has enabled). Thus, the final position differs from the initial position only in the absence from the board of the black pawn e4 and neutral Nao c8. When in the twin the black pawn is on the square f3 instead of f2, then the neutral Nao c8 captures the pawn on e4, with it’s place being occupied by the neutral Vao. And, finally, the cycle is closed with a pawn on f4 – the pawn e4 is captured by the neutral Vao a8, but its a8 square is occupied by the neutral Pao. How lovely!

270: a) 1…nNh4-f8 2.nQd6×d4 ncQg7×d4=ncS + 3.ncSd4-e6=ncB ncBe6-a2=ncR #; b) 1…nQd6-h2 2.nNh4×g2 ncRg7×g2=ncQ + 3.ncQg2-d2=ncS ncSd2-b3=ncB #
An amazing collaboration between 3 neutral pieces – nQd6, nNh4, and Chameleon g7 – in the creation of two different battery mates. In a) the battery is created on the line f8-с2 and the rear piece is the N which moves to f8. Then a neutral Q, capturing on d4, allows a capture by cQ on the same square, with a transformation of cQ to cS, thus checking the black King. Black defends by moving this cS, but leaving is possible only along the pin-line, where cS transforms into cB which becomes the forward piece of the battery. In conclusion, White opens the battery line with a move by cB to a2, where cB transforms into cR and in this way gives mate with double check.
The twin b) has absolutely the same content, but the main role is played by a battery on the line h2-с2, and the rear piece is the nQ. The forward piece begins on the g2 square and moves along the pin-line to become cS, finally transforming into cB in the double-check mate.
The beauty is complemented by the method of creation of the twin, which seems to be part of one cycle. In a) cQ transforms into S, B, R, but in b) the transformation continues from R to Q, S, B.
It should also be noted that White has the first move, and this can’t be changed – if Black were to begin then it would lead to either self-pin or self-check. Bravo!

No.227 Daniel Novomesky Slovakia Julia’sFairies – 2013/I 4th Prize 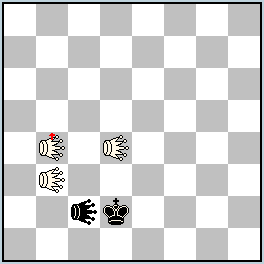h#5                                                (3+2) b) Twin Shift a1 b1 c) Twin Shift a1 b3 d) Twin Shift a1 c5 Royal Double Grasshopper b4 Double Grasshoppers: b3, d4, c2

No.231 Václav Kotěšovec Czech Republic Julia’sFairies – 2013/I 5th Prize h#7              3 solutions             (2+3) PWC Grasshopper g1 Kangaroo f4

4th Prize: No. 227, Daniel Novomesky

a) 1.Kd2-c3+ rDGb4-d5 2.Kc3-b2 DGd4-c3 3.Kb2-a1 rDGd5-c4 4.DGc2-d4 DGc3-e3 5.DGd4-b2 DGb3-d3#; b) 1.Ke2-f3 rDGc4-f5 2.DGd2-f4 DGc3-e3+ 3.Kf3-g2 DGe4-g1 4.Kg2-h1 DGg1-f2 5.DGf4-g2 DGf2-f4#; c) 1.Ke4-d5+ rDGc6-c3 2.Kd5-c6 DGe6-d6 3.Kc6-b7 DGc5-c4 4.Kb7-a8 rDGc3-c7 5.DGd4-b7 rDGc7-c5#; d) 1.Kf6-g6 rDGd8-d5 2.DGe6-g8 rDGd5-d6 3.DGg8-g7 DGd7-f5 4.Kg6-h7 DGf8-f6+ 5.Kh7-h8 DGf6-e6#

Unusual pieces, unusual twinning mechanism, but also extraordinary pleasure caused by the content of the problem! Precise interaction between the black King and three white DGs, including Royal DG, leads to four echo-mates with the black King in all four corners of the board. While two white pieces take away two orthogonal squares from the black King (in a diagonal-orthogonal route), the third gives mate in an orthogonal-diagonal direction. The only diagonal square of the black King is blocked by his own DG. Strict analogy between the solutions of the four (!) twins. And all of this with five pieces only!

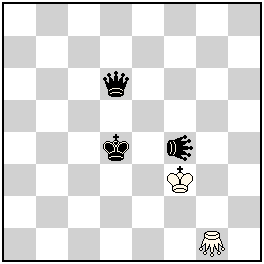
5th Prize: No. 231, Václav Kotěšovec

I. 1.Kc3 Ke4 2.Qd4+ K:f4(KAe4) 3.Q:g1(Gd4) Ke5 4.Kb2 K:e4(KAe5) 5.Ka1 Kd3 6.Qb1+ Kc3 7.KAb2 Kb3#; II. 1.Qd7 K:f4(KAf3) 2.Kc5 Ke5 3.Kb6 Ga7 4.Q:a7(Gd7)Kd6 5.Kb7 Gd5 6.Ka8 Kc6 7.KAb7 Kc7#; III. 1.Qb6 Kg4 2.Ke3 Kf5 3.Kf2 Ke4 4.Kg2 K:f4(KAe4)5.K:g1(Gg2) Kf3 6.Kh1 G:e4(KAg2) 7.Qg1 Kg3#

Three marches of the black King to three different corners of the board, with subsequent occupation by Q and KA of two orthogonal squares on a line with the white King (in this order, to avoid a check to the white King), finished with a mate by G on the diagonal. Good use of the properties of the fairy pieces and the applied fairy condition (PWC). Three solutions and only five pieces. Excellent!

No.220 Francesco Simoni Italy Julia’sFairies – 2013/I   6th Prize h#3               2 solutions              (6+5) Bishophopper a7, g8 Rookhopper c8, d8 Grasshopper h7

No.302.1 Pierre Tritten & Dmitri Turevski France / Russia Julia’sFairies – 2013/I Dedicated to Diyan Kostadinov 7th Prize h#2               3 solutions           (0+11) Anti-Andernach Take & Make KoBul Kings

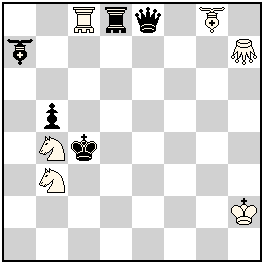
6th Prize: No. 220, Francesco Simoni

I. 1.Qe4 (Qc6 ?) Gd3 (Gf5 ?) 2.Qc6 (Qe6 ?) Sc5 (Sc1 ?) 3.BHd4 (RHd4 ?) Sd5‡; II. 1.Qg6 (Qe6 ?) Gf5 (Gd3 ?) 2.Qe6 (Qc6 ?) Sd5 (Sa2 ?) 3.RHd4 (BHd4 ?) Sc5‡

Similar creation of anti-battery mates during both solutions. In the first solution mate is given by the Bishop-Hopper, and the Rook-Hopper pins the black Q, but in the second solution the opposite occurs. The location of the white pieces in the final positions is almost identical, it differs only in the control of c5 and d5 squares by the white G. But for that G to be able to get this control, the help of the black Q is needed. That is why bQ on the first move provides a hurdle, but in such a way so that it can pin itself on the second move. Only after that can Black block d4 square, one time by the Bishop-Hopper and the other time with the Rook-Hopper. White should use the hurdle offered on the first move to jump with the G, and only after create vertical and diagonal anti-batteries by alternating moves of Knights to c5 and d5. Model mates. Simply – a beauty!

7th Prize: No. 302.1, Pierre Tritten & Dmitri Turevski

I. 1.Bc6(W) B×b5(Bf7) 2.NKa6 B×c4(Bc8)‡; II.1.Nd6(W) N×c4(Nb4)+ 2.RKh2 N×h1(Nf3)‡; III.1.Rh4(W) R×h1(Rd5) 2.BKh7 R×b5(Rh8)‡

Three black pieces in three solutions cyclically change their functions. Each one starts a solution, and by anti-Andernach changes its color. It then captures another piece, whose mobility is given to the black King by KoBul, and by Take&Make is moved to a square from where it attacks the 3rd piece. Finally on the mating move it captures the 3rd piece, changing the mobility of the black King for a second time and with a Take&Make move gives a model mate to the King. Beautiful!

No.292.1 Petko A. Petkov Bulgaria Julia’sFairies – 2013/I Dedicated to the 1st Jubilee of Julia’s Fairies 8th Prize hs#2*            2 solutions            (4+8) Chameleon Rh1 PAOs: c8, h8; VAO g8 Grasshopper e8

No.273 Ivan Skoba & Ján Golha Czech Republic / Slovakia Julia’sFairies – 2013/I   9th Prize pser-h#12     b) bKh7->a7         (2+2) Vertical Mirror Circe

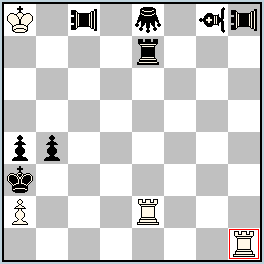
8th Prize: No. 292.1, Petko A. Petkov

Set-play: 1…VAc4 2.CRc1=CQ+ PAxc1#; I. 1.CRh5 = CQ PAc6 2.CQb5 = CS+ Gxb5#; II. 1.CRh4 = CQ Ge6 2.CQc4 = CS+ VAxc4#

A black half-battery in which one of the three half-battery pieces  creates a hurdle, another one uses this hurdle in the final jump, with the PAO h8 giving mate using the third piece as a hurdle. The roles of all three pieces are changed cyclically. At the same time the white Chameleon goes to a square from where it can give the final check. Solid content, good construction, a pleasant experience.

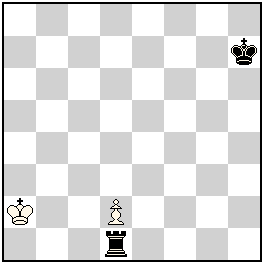
9th Prize: No. 273, Ivan Skoba & Ján Golha

a) 1.Ra1+ Kb3 2.Ra3+ Kc4 3.Rc3+ dxc3 [+bRa8] 4.Ra4+ Kd5 5.Rd4+ cxd4 [+bRa8] 6.Ra5+ Ke6 7.Re5+ dxe5[+bRa8] 8.Ra6+ Kf7 9.Rf6+ exf6 [+bRa8] 10.Rg8 11.Rg7+ fxg7 [+bRa8] 12.Rh8 gxh8R [+bRa8] #;
b) 1.Rxd2 [+wPe2]+ Kb3 2.Rd3+ exd3 [+bRh8] 3.Rb8+ Kc4 4.Rb4+ Kc5 5.Rc4+ dxc4 [+bRh8] 6.Rh5+ Kd6 7.Rd5+ cxd5 [+bRh8] 8.Rh6+ Kc7 9.Rc6+ dxc6 [+bRh8] 10.Rb8 11.Rb7+ cxb7 [+bRh8] 12.Ra8 bxa8R [+bRh8] #

The black Rook helps the white King and pawn to gradually move to the other end of the board. For the support provided and in the honor of the black Rook, the pawn also promotes into Rook. But here the love is over, and the promoted pawn  suddenly gives mate to the black King! In a) King and pawn travel to the north-east, but in b) – to the north-west, but always close to their black colleague. The fairy stipulation and condition are well chosen.

No.214 Petko A. Petkov Bulgaria Julia’s Fairies – 2013/I 1st-2nd Honorable Mention ex aequo 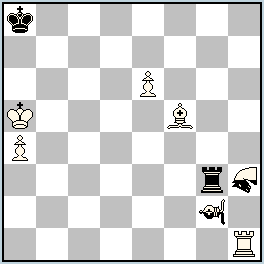hs==5           2 solutions        (5+2+2) KoBul Kings Nightrider-Locust h3 Bishop-Locust g2

No.224 Petko A. Petkov Bulgaria Julia’s Fairies – 2013/I 1st-2nd Honorable Mention ex aequo 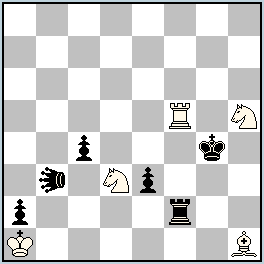hs#4              2 solutions            (5+6) Leo b3

1st-2nd Honorable Mention: No. 214 and 224, Petko A. Petkov

214: I. 1.Bg6! Rxg6 (Ka5=rB) 2.rBd2 Rxe6 (rBd2=K) 3.Re1 Re4! 4.nLBxe4-d5 (Ka8=rR) rRd8 5.nLNxd5-b6 (rR= rLB) rLBxb6-a5(Kd2= rLN) ==; II. 1.Bg4! Rxg4 (Ka5=rB) 2.rBc3 Rxa4 (rBd2=K) 3.Rb1 Rf4! 4.nLNxf4-d5 (Ka8=rR) rRa5 5.nLBxd5-c6 (rR= rLN) rLNxc6-e7 (Kc3= rLB)==

Two similar solutions, where in the final position only the white pawn, white Rook and two Kings remain on the board. The pawn can’t move as it is blocked by the black King; the Rook is pinned as a move would endanger his own King, who also can’t move because he has no piece to capture. The black King would have a move, but the white Rook prevents him from doing so. One King has received the mobility of Locust-Bishop, while the other has Locust-Nightrider; but in the other solution the Kings have amicably exchanged these properties. Rich content, perfect harmony!

224: I.1.Ra5!! LEb5! 2.Sdf4 (not 2.Bd5?) LEg5!! 3.Bd5! Kf5 4.Bf3 + LExa5 #; II. 1.Ba8!! LEb7! 2.Sc1 (not 2.Rd5?) LEg2!! 3.Rd5! Kf3 4.Rd4 + LExa8 #

Critical moves of the white Rook and Bishop have a triple motivation: to cross the critical square d5, to open a line for the black Leo and to prepare for the final capturing move. White must choose the order of moves very precisely, because he can go to d5 only after this critical square has been crossed by the black Leo. The self-mate finale is very interesting. After the black King’s move to the free square provided to him by White as a result of the interference on the square d5, there follows a check from the newly-formed white battery, against which there is no defense other than the capture of the rear battery piece – on the same square it went to on the 1st move! Excellent construction (only 11 pieces) and model mates (although practically identical – the only difference is in the position of the black Leo on the “a” file).

No.230 Václav Kotěšovec Czech Republic Julia’s Fairies – 2013/I   3rd Honorable Mention #2                                                 (9+9) b) Anti-Andernach Royal Zebra f3 Rookhoppers: a6, e5, h1 Bishophoppers: d5, f8

No.276 János Mikitovics Hungary Julia’s Fairies – 2013/I Dedicated to Petko A. Petkov in occasion of his birthday! 4th Honorable Mention 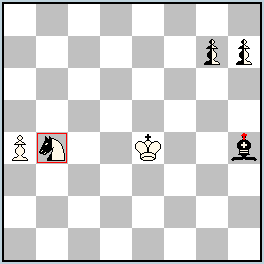pser-h=5     2 solutions         (2+1+3) Chameleons: Sb4; Royal Bh4 Symmetry Circe KoBul Kings

3rd Honorable Mention: № 230, Václav Kotěšovec

The black Zebra King (I do not like the name “Royal Zebra” and similar terms) can theoretically move to four squares – c1, c5, d6 and h6, which in the initial position are under White’s control. So after self-blocks on these squares, the white pieces guarding them can leave this control and mate the black King. It is interesting how the situation changes in the twin. The weakening effect of the black defences is not blocking, as the color of the piece changes after its move, but the attack of one of the King’s other squares. While in twin a) the square c1 is blocked, in twin b) the same defence takes control of the square c5. There is thus a cycle of alternating weakening motifs for all four defences. The cyclic interchange of the four mates is achieved by changing the orthodox conditions to Anti-Andernach. The author had probably already patented this idea in problem 5749 in Phénix 175, 2008 with a change of five mates, and in the beautiful 1313 РАТ А МАТ 2009, with a cyclic change of even six mates. (A note to 230.1: of course, six is more than four, but the cycle is lost in the abundance of different fairy pieces.)

4th Honorable Mention: No. 276, János Mikitovics

I. 1.ncSb4-c6=ncB + rKe4-f5 2.ncBc6-b5=ncR + a4xb5 [+ncRg4] [brcB=rcR] + 3.rcRh4xg4=rcQ [wrcK=rcR] + rcRf5-e5=rcQ 4.nPg7-g5 5.rcQg4-h5=rcS nPh7-h8=ncS!! = ; II. 1.rBh4-e7 2.ncSb4-d3=ncB + rKe4xd3 [+ncBe6] 3.rcBe7-d6=rcR + rKd3-c2 4.rcRd6xe6=rcQ [+ncBd3] [wrcK=rcB]+ ncBd3-e4=ncR + 5.rcQe6-g6=rcS nPh7-h8=ncB!! =

A rich combination of not so common, but very well used, fairy elements. The Bishop-Chameleon-KoBul King (not too many functions for the one poor King?☺) finally transforms into S, not able to move as all squares where it might go are under White control. The other pieces also can’t move – one neutral pawn is one time pinned, the second time blocked, and the other neutral pawn will transform into an immobile S or B, while the Chameleon is previously captured or pinned. Oha! ☺(Very good!)

No.221 Valerio Agostini Italy Julia’sFairies – 2013/I 5th Honorable Mention 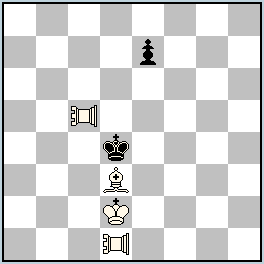h#2                2 solutions             (4+2) Pao c5, d1

No.259.1 Gani Ganapathi India Julia’sFairies – 2013/I 6th Honorable Mention 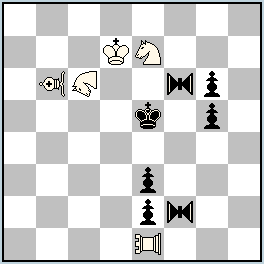h#2,5            2 solutions             (5+7) Equihoppers: f2, f6 PAO e1; VAO b6; NAO c6

5th Honorable Mention: No. 221, Valerio Agostini

I. 1.e5 PA-a5 2.e4 Bb5≠; II. 1.e6 PAc-c1 2.e5 Bc2≠

Horizontal and vertical critical moves of the white PAO and blocking of the appropriate squares of the black King ends with a battery mate. The lone black pawn helps the white B and PAO. Simple construction, miniature, harmonious content.

6th Honorable Mention: No. 259.1, Gani Ganapathi

I.1…NAb8 2.EQ2d4 VAxe3 3.EQh6 VAxh6#; II. 1…VAd8 2.EQ6d4 NAxe2 3.EQh8 NAxh8#

Two battery mates, where the rear piece is the white PAO and the forward piece is the VAO and NAO alternately. Where the battery is fired by the VAO, the NAO takes control of the square f6 of the black King, and vice versa. One black Equihopper, with a move to d4, helps the Chinese pieces to create a battery, while the other one – with a move to a square where it can be captured – to fire it. Furthermore, the firing piece also controls the square f4. Perfect cooperation of all pieces. Position 259.1 is better than 259: a half-move longer, one piece fewer, and fairy pieces are better utilised. 

No.237 Mario Parrinello Italy Julia’sFairies – 2013/I 7th Honorable Mention 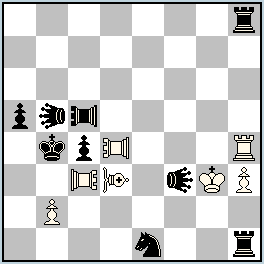hs#4             2 solutions              (7+9) Locust f3 Rook-Locust c3 Bishop-Locust d3 Siren b5 Tritons d4, c5

No.298 Georgy Evseev, Petko A. Petkov & Julia Vysotska Russia / Bulgaria / Latvia Julia’sFairies – 2013/I 8th Honorable Mention 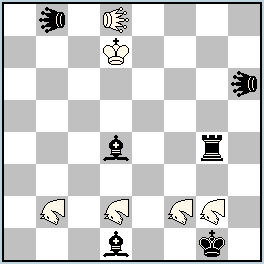h#3               2 solutions             (6+6) Lions: b8, h6 Kangaroos: b2,d2,f2,g2 LEO d8

7th Honorable Mention: No. 237, Mario Parrinello

I. 1.TRg4 Lxg4-h5 2.Rg4 TRg5 3.LRxc4-c5 + SIc4 4.LRxc4-c3 + Lxg4-f3 #; II. 1.TRf4 Lxf4-f5 2.Rf4 SIb8 3.LBxc4-b5 + TRc4 4.LBxc4-d3 + Lxf4-f3 #

Beautiful interaction of the Locust family with their close relatives – Marine pieces – with almost identical motivation of the corresponding moves in both solutions. What happens in one solution diagonally, happens in the other orthogonally, and vice versa. I was impressed by the return theme and the way in which both White and Black construct the special batteries, which are fired by the capture of the forward piece. Amazingly, at the end of this rich content both final positions are completely identical, differing only in the position and type of the mating piece. However, more complex than a discussion of the content of this task was to determine which position is better – 237 or 237.1. It is definitely better to use a pawn instead of a Triton whose only duty is to sacrifice itself on the front two squares. But at what cost? In 237.1 not only is the Triton replaced by a pawn, but a white S and three black pawns are added. The position became increasingly congested so I therefore decided to award No.237.

8th Honorable Mention: No. 298, Georgy Evseev, Petko A. Petkov & Julia Vysotska

I.1.Rxg2 LEb6 2.LIxb2 KAa7+ 3.LIf2 LEb1#; II. 1.Bxf2 LEg5 2.LIxd2 KAg6+ 3.LIg2 LEc1#

The four Kangaroos on the second rank alternate in the performance of their functions with amazing precision. In the first solution Kangaroo g2 is captured by Black, blocking this square, while Kangaroo f2 fires a battery check from the white LEO. In the second solution exactly the opposite occurs. The roles of the other two Kangaroos are interchanged in the same way – while one is captured by Black, opening a line for the white Leo, the other one controls King’s square h2. Very nice, but it should also be noted that in each solution one black Lion is not needed.

No.300 Michel Caillaud France Julia’sFairies-2013/I Dedicated to the 1st Birthday of Julia’s Fairies! 9th Honorable Mention 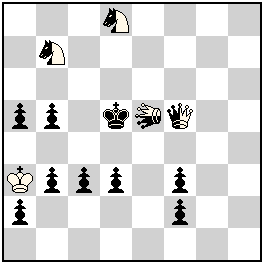h#3               2 solutions        (1+9+4) Neutral LEO e5

No.307 Mario Parrinello Italy Julia’sFairies-2013/I Dedicated to the 1st Birthday of Julia’s Fairies 10th Honorable Mention 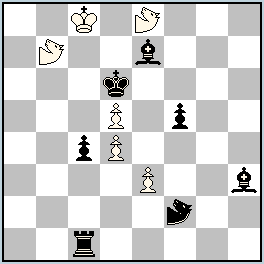h#2              b) MSf2→e1           (6+7) Marine Knights: b7, e8, f2

9th Honorable Mention: No. 300, Michel Caillaud

I. 1.nSc6 nQ×f3+ 2.nLEe4 nQh1 3.nLEg2 nLE×a2‡; II. 1.nSd6 nQ×d3+ 2.nLEd4 nQd1 3.nLEd2 nLE×a5‡

Very good orthogonal-diagonal analogy in all the moves of both solutions, exemplary cooperation of the neutral Q and LEO, two model mates.

10th Honorable Mention: No. 307, Mario Parrinello

a) 1.MSg4 MSa5 2.MSxe3-c2 MSxc4-e3 #; b) 1.MSc2 MSg7 2.MSxe3-g4 MSxf5-e3 #

The black pawns c4 and f5 are pinned in a special way, because after their move the black King would be in self-check from the Marine Knights b7 and e8. But if those pawns are removed then not only would the black King be in check, so would the white King. So there comes a “moment of glory” from the black Marine Knight f2. It unblocks the square e3 by capturing the pawn on it, and interferes with a black piece aimed at the white King – one time on c2, the other time on g4. Good analogy with a solo of Marine Knights in the play of both sides.

No.249 Julia Vysotska Latvia Julia’sFairies-2013/I 1st Commendation 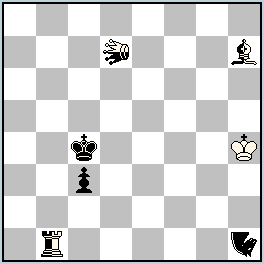h#2,5        b) +black Pd4     (1+3+3n) Nightrider h1 Locust d7

No.252 Julia Vysotska Latvia Julia’sFairies-2013/I 2nd Commendation 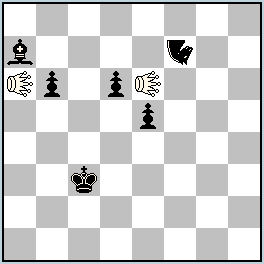h#3               2 solutions            (2+6) (no w.King) Nightrider f7 Locust a6, e6

1st Commendation: No. 249, Julia Vysotska

a) 1…nBh7-e4 2.Nh1-b4 nBe4-d5 + 3.nLd7xd5-d4 nRb1xb4 #; b) 1…nRb1-b6 2.Nh1-d3 nRb6-c6 + 3.nLd7xc6-b5 nBh7xd3 #

A problem with two interesting mating finales, where the neutral Locust not only controls most of the squares of the black King, but also pins the mating piece, which occupies one of those squares. There is an interchange of captured and mating pieces (Zilahi theme). In position a) the pawn c3 is not needed, but in position b) one more pawn is needed.
This problem caused a very big creative debate on the site. My point of view here is as follows: An increase in the number of moves is justified only when every added move is an integral part of the specific thematic complex, expands the author’s intention, or is a carrier of an individual interesting effect. The moves 1…nВh7-e4 and 1…nRb1-b6 only partly fulfill these conditions. The use of fairy pieces is justified only if they participate in the thematic content of the problem. If the same result can be reached with orthodox pieces, then the use of fairy pieces is meaningless. Of course, there are some exceptions. In No.249 the Nightrider can be replaced with a Q.
Every artistic work, including a chess problem, has its content and form. Personally, I give much more attention to the content of the problem than to its construction, and especially appreciate the originality of the author’s intention, motivation and ideological wealth of individual moves, and the relationship of all thematic elements. The content of problem No.249 I consider  very original and exceeds the mentioned constructional flaws. Therefore I have decided to award the problem.

2nd Commendation: No. 252, Julia Vysotska

1.Kc3-b4 Le6xd6-c6 2.Nf7-b5 Lc6xb5-a4 + 3.Kb4-a5 La6xa7-a8 #; 1.Kc3-d4 La6xb6-c6 2.Ba7-c5 Lc6xc5-c4 + 3.Kd4-d5 Le6xf7-g8 #

An attractive orthogonal-diagonal analogy between the two solutions, ending with model battery mates. Additional black material is used for the white Locusts’ moves (who must capture), and finally not more than five pieces are left on the board. Black pawns do not always have to play, and pawn e5 in the first solution is resting.

No.234 Pierre Tritten France Julia’sFairies-2013/I 3rd Commendation 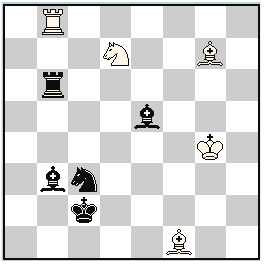 h#2              3 solutions             (5+5) Take & Make

No.243 Peter Harris South Africa Julia’sFairies-2013/I 4th-10th Commendation ex aequo  ser-hs#6       b) Kh8→g8           (2+1) Haaner Chess Super-Circe Chameleon Chess

3rd Commendation: No. 234, Pierre Tritten

I. 1.Ba4 S×b6(Sb3) 2.K×b3(Ka5) B×e5(Bc7)‡; II. 1.Sa4 B×e5(Bc3) 2.K×c3(Ka5) S×b6(Sc6)‡; III. 1.Sd5 S×e5(Sc3) 2.K×c3(Ke4) R×b6(Re6)‡

While for the first two solutions it is possible to say that all motifs there are absolutely analogical, this can’t be said about the third solution. However, with this material and in the given position it would be very difficult to achieve complete analogy. It looks like analogy would be easier to find not in the previous two, but in a fourth solution. But still, in this tournament three solutions are not so common, so such a problem should be awarded.

4th -10th Commendations:
No. 243, Peter Harris

a) 1.b2-b1=S 2.Sb1-a3=B 3.Ba3-e7=R 4.Re7*f7=Q[+wPh6] 5.Qf7-g8=S h6-h7 6.Sg8-f6=B #; b) 1.b2-b1=B 2.Bb1-c2=R 3.Rc2-f2=Q 4.Qf2*f7=S[+wPg7] 5.Sf7-h8=B Kg8*h8 [+bBg1] 6.Bg1-h2=R #

Only three pieces, but three fairy elements have allowed the author to create twins with analogical solutions. In the first twin a series of moves starts with a black pawn, promoted into S, which gradually makes the whole cycle of transformations to finally appear again in “Knight’s skin”, then makes the last move to transform into B and give mate to the white King. In the second twin the cycle of transformations is shifted by one piece – it starts from the promotion into B, and ends with a move of B and transformation into R. One King’s square, thanks to Super-Circe, is blocked by the white pawn, but the second King’s square doesn’t exist anymore thanks to the second condition.

No.256 Peter Harris South Africa Julia’sFairies-2013/I 4th-10th Commendation ex aequo 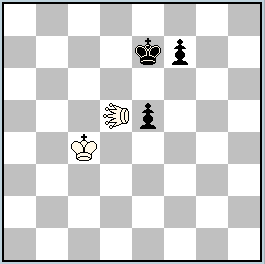 hs#2             2 solutions              (2+3) Transmuted Kings Super-Circe Locust d5

No.277 Chris Feather England Julia’sFairies-2013/I 4th-10th Commendation ex aequo 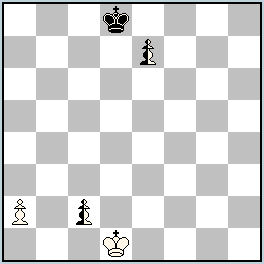 h#2              3 solutions        (2+1+2n) Anti-Kings+Anti-Circe

No. 256, Peter Harris

I. 1.Ld5xe5-f5 [+bPd1=bR] Rd1-d3 2.Lf5xf7-f8[+bPf1=bL] + Rd3-d6 #; II. 1.Ld5xe5-f5 [+bPg1=bB] Bg1-c5 2.Lf5xf7-f8[+bPc1=bL] + Bc5-d6 #

The same first and second moves of the white Locust, but with captured pawns promoting on different squares. A diagonal Locust/Rook battery, targeting the white King, is changed to vertical Locust/Bishop, but the firing battery pieces both times go to d6. From a theoretical point of view, please pay attention to the form of the defensive motive of these moves. A check to the black King is parried by blocking, which is impossible in orthodox chess. A very ingenious and original problem.

№ 277, Chris Feather

I. 1.nPc1=nR Pa3 (Pa4? … 3.nRxa4[nRa8]!) 2.nRa1 nPe8=nQ#; II. 1.nPc1=nS+ Ke2 2.nSxa2[nSg8]+ nSxe7[nSg1]#; III. 1.nPc1=nB+ Kd2 2.nBa3+ nBxe7[nBc1]#

An interesting presentation of the new fairy condition. I have given preference to problem 277 over 278 because of the three different promotions by the same neutral pawn. But I must remind you that the name “Anti-King” does not show the essence of the difference from orthodox chess. It does not change the King’s move (his mobility is the same as in orthodox chess), but the aim of the play is changed, so it is not “Anti-King”, but “Anti-Check”.

No.279 Pierre Tritten France Julia’sFairies-2013/I   4th-10th Commendation ex aequo 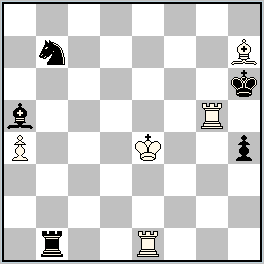h#2               2 solutions             (5+5) Take & Make

No.293 Petko A. Petkov Bulgaria Julia’sFairies-2013/I Dedicated to the 1st Jubilee of Julia’s Fairies 4th-10th Commendation ex aequo  h#2             b) Kh2→f1       (4+10+4) Take & Make Neutral Nightriders: f4, h8

№ 279, Pierre Tritten

I. 1.R×e1(Re3)+ K×e3(Kb3) 2.K×h7(Kb1) R×a5(Re1)‡; II. 1.B×e1(Be3) K×e3(Ka7) 2.K×g5(Ka5) B×b1(Be1)‡

Gorgeous orthogonal-diagonal model echo-mates with an interesting creation. One of the black pieces, capturing the white Re1, goes to e3, where the white King captures it and thus prepares the mating finale. The black King with the same aim captures one of the remaining two white pieces on the board (Zilahi). And the last white piece, capturing the second black piece, returns to e1 again! This beautiful “spectacle” is repeated in the two solutions, with an alternation of the pieces involved!

№ 293, Petko A. Petkov

a) 1.nNxh5-h6+ nRf4! 2.nNb3 nBxf4-f1#; b) 1.nNxg2-g4+ nBf4! 2.nNe8 nRxf4-e5#

The white King is targeted by the neutral-Bishop (in the twin – neutral-Rook) battery, the black King by the neutral-Nightrider half-battery, and the whole content of the problem lies in their interaction and the play on the f4 square. When the neutral Nightrider f4 as the firing piece leaves the f4 square with a check to the white King, one of the forward pieces of the half-battery intercepts the check on the same square. And finally the other piece, on the same square again, captures the first one, opening a battery check to the black King and, leaving the f4 square by Take&Make rules, gives the black King a second check. Mutual interference on the f4 square (Grimshaw theme) on the first move changes into mutual capturing with mate (Zilahi theme) on the second move. Very interesting.

No.304 Luis Miguel Martín Spain Julia’sFairies-2013/I 4th-10th Commendation ex aequo 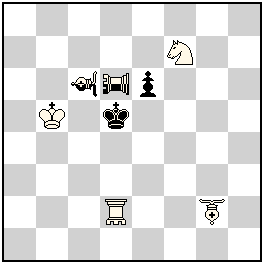 h#2            2 solutions          (4+2+2) Rookhopper d2 Bishophopper g2 Neutral Contra Rookhopper d6 Neutral Contra Bishophopper c6

No.308 Vito Rallo Italy Julia’sFairies-2013/I 4th-10th Commendation ex aequo 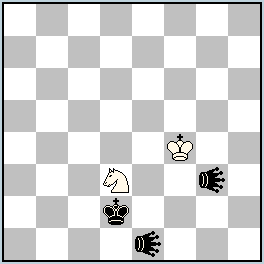h#4,5             b) Sd3→e2             (3+3) Andernach-Grasshoppers: g3, e1

№ 304, Luis Miguel Martín

I. 1.nCRHd3 nCBHe4+ 2.nCBHb7 BHc6#; II. 1.nCBHf3 nCRHd4+ 2.nCRHd7 RHd6#

A problem with rarely met fairy pieces and with two interesting Zabunov-variations. The neutral Contra Bishophopper and Contra Rookhopper alternate in performing the functions of mating piece, and hurdle allowing control of King’s squares (d4, e4).

№ 308, Vito Rallo

a) 1…Kf4-e5 2.AGg3-d6 Ke5-e4 3.AGe1-e5 Sd3-f2 4.Kd2-e1 Ke4-e3 5.AGd6-f4(wAGe5) AGe5-g3(wAGf4) #; b) 1…Kf4-g5 2.AGe1-h4 (wAGg3) AGg3-g6 3.Kd2-e1 Kg5-f4 4.AGh4-e4 Kf4-f3 5.Ke1-f1 AGg6-d3 (wAGe4) #

A mirror echo, in which the main “engine” of all the changes is the white King.

 2013-IJanuary-April’2013

In conclusion, I thank Julia for the invitation to judge this exceptional competition, congratulate the authors of the awarded problems and apologize to all those who think that I’ve underestimated their problems.

Juraj Brabec,
International judge of FIDE for chess composition

Bratislava, May 2013.

Appendix to Preliminary AWARD JULIA’S FAIRIES 2013/I:

The 9th Prize (No.273, Skoba & Golha) is partially anticipated by Cornel Pacurar, PS2514F, The Problemist Supplement 09/2011. No.273 therefore loses its prize and instead receives 4th-11th Commendation. The Award now becomes final.

(see more in the post from July, 19th, 2013)