Disparate – PART I (P.A.P.)

PART I – General rules for the white and black pieces

Definition

Disparate: If one side makes a move with a piece of type “x” (black, white, neutral, half-neutral, etc., King included), the other side cannot answer immediately by moving a piece of the same type “x”!

All these enemy pieces of type “x” are in a state of “half-move paralysis – HMP” (this is my term) which immediately vanishes after realisation of the following half-move from the other side, using a piece of another type “y”!

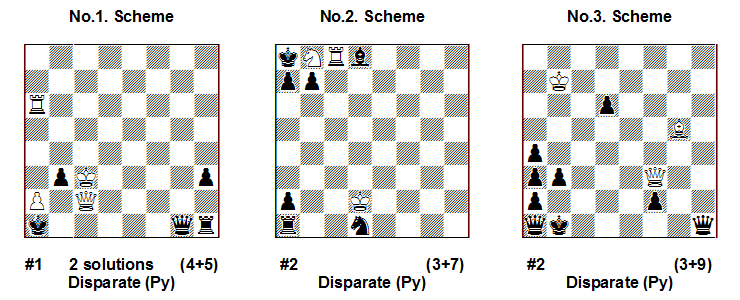
In Scheme No.1 the white piece in role “x” is Qc2, the black opponent of the same type “x” is Qg1. After 1.Qc1#! we have mate because according to the definition Qg1 is paralysed (HMP) and cannot answer with 1…Qxc1. Incorrect is 1.Qd1+?? because Black has a powerful answer – 1…Kb2#!! – mate to the white King because it is paralysed by the black King!
Of course, here White can also play 1.Kb2#! – with paralysis of the black King!
There is also an interesting try: 1.axb3+? with play of the white Pa2/Ra5 battery. But Black has a very good thematic defence: 1…Rh2!! and Ra5 is paralysed (HMP)!

In Scheme No.2 after 1.Sc6+? Black answers with 1…Rb1!! and Rc8 is paralysed! (of course, not 1…Rc1? 2.Kxc1#! because Rc8 is then no longer under paralysis). Interesting is 1.Sd7+? but after 1…Rb1!! the double-check 2.Sb6?? is not mate because 1…Rxb6!! and Rc8 is once again paralysed! The solution is 1.Sa6+! and if 1…Rb1 (Rc8 is paralysed) then 2.Sc7#!! – mate through double check because the Rc8 is not longer under paralysis! An interesting defence is 1…Rc1 – now 2.Sc7?? is not mate because 2…Rxc7!! and Rc8 is again under HMP, but now 2.Kxc1#! with a new activation of the white Rc8!

In Scheme No.3 the solution is: 1.Qd1+! – self-unpin of the white Q, paralysing the black Qh1. 1…Kb2+! – now Qh1 is again activated and gives check to the white King (2.Bf6?? is not possible here!). But there follows: 2.Qc1#!! – Qh1 is again paralysed, also paralysed is Qa1 – therefore the defences 2…Qhxc1 and 2…Qaxc1 are illegal!
Some white tries are of interest: 1.Qc6!? – now both black Queens are paralysed, the white threat is 2.Qc1#! – with continuing paralysis of Qh1. After 1…b2 Qh1 is again activated but White’s answer is 2.Qe4#! (Qh1 is again paralysed!). But Black has a good defence: 1…f1=R!! (2.Qc1+? Rxc1!). Analogical play is seen after 1.Qc3? b2+ 2.Qd3# but 1…f1=R!
An non-standard try is 1.Qxf2!? – zz – now both black Queens are paralysed and Black can play only with his Pawns: 1…b2+ (Qh1 is activated) 2. Qf5#! (Qh1 is again paralysed!) but 1…d5!!

Now follows many light but instructive examples by the inventor.

In No.4 at first glance the stipulations seem very strange. Here the white King completely dominates against his black colleague – after every move the w.K paralyses the black Kh3 which remains static until the end of play due to HMP! a) 1.Ke6! a5 2.Kf5 a4 3.Kg4#! ; b) 1.Kc6 a5 2.Kb5 a4 3.Kxa4=!

In No.5 after 1.Bd2! the threat is 2.b5# – pay attention that after the key-move the Bg6 is paralysed and cannot play 1…Be8 or 1…Bd3. 1…e5! – now Pb4 is paralysed and Bg6 is activated! 2.Bc3! (Bg6 is paralysed, Pb4 is activated) 2…e4 3.Bd2 e3 4.Bc3 e2 5.Bd2 Se1~ 6.b5# – a duel between two pairs of pieces – Be3,Pb4 against Bg6,Pe6.

In No.6 we see a nice model mate after two Queen promotions: 1.Ka3! a8=Q 2.Ka4 Qh8 3.b1=Q Qa1# – mate because the black Queen is paralysed by the w.Q. Tries: 1.b1=Q? but 1…b8=Q is impossible because Pa7 is under HMP. Of course, 2.b1=Q is also illegal.
By the by, it is possible to solve this problem in 2,5 moves after 1…a8=Q 2.Ka3! (not 2.b1=Q?) 2…Qh8 3.b1=Q or 3.b1=S Qa1#, but Black does not have a tempo-move! Of course, because of the analogy with the real solution and the duals in promotions (3.b1=Q and 3.b1=S) we cannot claim that there exists a complete set-play.

In No.7 we have to find the right order of white and black moves. I.1.Bb1 exf8=B 2.Rb2 Bxd6 3.h1=B Be5=! A very interesting finale – a single white Bishop paralyses three black Bishops and pins the black Rook! Wrong is 1.Rb2? exf8=B 2.Bb1? and 2…Bxd6 is illegal; after 2.h1=B? Bxd6 3.Bb1? is illegal. Another try is 1.h1=B? but 1…exf8=B? is illegal because Pe7 is under HMP. II. 1.Rb2 exd8=R 2.Bb1 Rxd6 3.h1=R Rd1=! Because of the white R-promotion it is wrong to begin with 1.Bb1? exd8=R 2.Rb2? and 2…Rxd6 is illegal, etc.

In No.8 the Bristol theme is twice realised (in opposite directions!) by 3 black pieces. 1.Rh8 2. Rcg8 3.Qf8 4-8.Kf7 9.Qa8 10.Rb8 11.Rhc8 13.Kd8 and now the final is paradoxical – 13…f7= !! Stalemate – in this position all black pieces are walled, the black King has no moves and all black Pawns are immobile because of HMP!

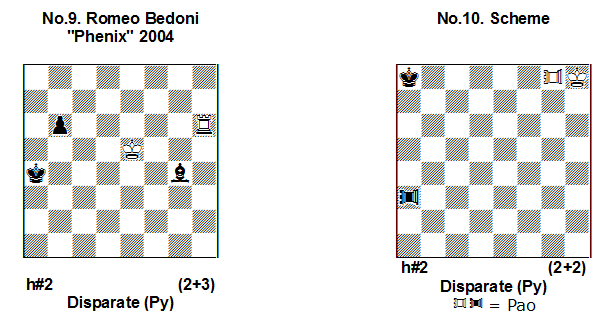
No.9 in elementary form presents a theme that has an important theoretical and practical importance: play of a battery that has a King as the forward (mating) piece! In this case the enemy King immediately comes under HMP and cannot make a move! 1.Kb5! Rh5 2.Be6 Kxe6#! – mate, because Kb5 is paralysed by its white opponent! Of course, here 1.Be6? Rh5 2.Kb5? is wrong – now Ke5 is under HMP and the move 2…Kxe6# is illegal!
Similar motives exist also in the play of anti-batteries.

In No.10 the white plan can be 1….Kg7 and 2….Kf8# (with HMP of Ka8) but it is not so simple to realise this idea. For example: 1. ~ Kg7 2.~ Kf8?? but 3.PA~!! and Ph8 is paralysed! An interesting sacrifice of PAa3 is needed: 1.PAf3! Kg7 2.PAf8!! – because PAg8 is under HMP from PAf8 the black King is not in check but follows: 2…Kxf8#!

Some special cases

a) Paralysis (HMP) after Pawn promotions

According to Disparate (Py) rules, if a Pawn realizes a promotion then this move is considered as a Pawn’s move, but not as a move of the promoted piece!
a) If before the Pawn’s promotion an enemy piece of type “x” (but not an enemy Pawn!) makes a move, the Pawn can be immediately promoted also to a piece of type “x”!
b) If a Pawn makes a promotion to a piece of type “x”, the enemy side can immediately answer with a move of a piece of the same kind “x”.

In Scheme No.11 White wants to mate with b8=S (it is a Pawn move, not a Knight move!!) but after b8=S+ Black could answer with Sa4~! and Sb8 is paralysed! Therefore it is necessary to play: 1.Sxb6! b8=S#! because here the b.S is pinned and cannot paralyse the w.Sb8.
In other words, here the piece of type “x” is the black S and after its move the Pawn mates with a promotion also to a piece of type “x”!

Another instructive example is No.12: I. 1.Bc2 a8=B+! (this move is possible because it is a Pawn’s move!) 2.Bb1!! (HMP of w.Ba8). Now follows mate after activation of Ba8 (destruction of its HMP) and capture of the black Bishop: 2…Kxb1#! This capture is needed because without the Annihilation of the black Bishop Black would have a defence on the third move 3.B~! with paralysis of Ba8. Analogically: II. 1.Qe2 a8=Q+! 2.Qb2+!! Kxb2#. An additional motif here is the black half-pin. There are model mates after specific play of the white “special battery” created from w.K as the forward piece and the promoted white piece as the rear piece!
Very interesting modifications are possible to this remarkable idea.

No.13: Analogical play to No.12 but here in three phases with a cycle of black half-pins and model-mates in Meredith form: I. 1.LIb8 a8=LI+! 2.LIf8! Kxf8#; II. 1.LEh5 a8=LE+! 2.LEf7 Kxf7#; III. 1.VAb5 a8=VA +! 2.VAd7! Kxd7#.

No.14 shows a task with 5 thematic solutions! I. 1.MOc3! b8=MO+! 2.MOe2!! Kxe2#! II. 1.Sc2 b8=S+ 2.Se1! Kxe1#; III. 1.MAh4 b8=MA+! 2.MAg2! Kxg2#; IV. 1.ROe6! b8=RO+! 2.ROg1 Kxg1#; V. 1.Nd6 b8=N+! 2.Nf2 Kxf2#. Here the “White super S-AUW” is combined with 5 Annihilation-captures by the white K after the thematic sacrifices of the black pieces! In the other words, here play 5 special batteries which have Kf1 as the forward piece. These batteries are: K/MO; K/S; K/MA; K/RO; K/N. The white King has two interesting features – it opens the special battery and paralyses his black opponent!

No.15 demonstrates cyclical creation of three anti-batteries with three thematic sacrifices and cyclical line-closings between black pieces: a) 1.LId2 h8=LE! 2.LEe8!! Kxe8# – K/LE anti-battery, LI/PAO interception. Thematic tries: 1.LEe8? but now after 1…h8=LE+? (it is a Pawn’s move of course!) Black cannot play LId2; also bad is 1.LEe8? Kxe8 2.LId2? h8=LE+? (a Pawn’s move again!) and follows 3.Ka7! (Kb7!); b) 1.PAb5! h8=LI! 2.LIf8 Kxf8# – K/LI anti-battery, PAO/LEO interception, thematic tries: 1.LIf8? h8LI+? and 1.Lif8? Kxf8 2.PAb5 h8=LI+? 3.Ka7! (Kb7!); c) 1.LEf4! h8=PA! 2.PAd8 Kxd8# – K/PA anti-battery, LEO/LI interception – thematic tries 1.PAd8? and 1…Kd8?. Model mates.

No.16 demonstrates another method for HMP of the thematic black pieces: pinning of these pieces! After 1.c7! there are possible 8(!) white promotions on b8 and c8 (4+4). But wrong is an immediate 2.c8=MA+? MAc2~!; 2.c8N+? Ne2~!, 2.c8S+? Sf3~!; 2.c8RO+? ROb3~!; 2.cxb8=LI+? LId2~!; 2.cxb8=LE+? LEf2~!; 2.cxb8=PA+? PAb4~!. The threat is only: 2.cxb8=G#! because in the initial setting a Grasshopper is pinned.
Black defences are unpins of Gc5 but self-pins of 7 black pieces on “d4”. There follow promotions by the Pc7 to the type of the pinned pieces: 1…MAxd4 2.c8=MA# – the defence 2…MA~! with HMP of white MAc8 is no longer possible! Analogically: 1…Nxd4 2.c8=N#!; 1…Sxd4 2.c8=S#!, 1…ROxd4 2.c8=RO#!, 1…LIxd4 2.cxb8=LI#!, 1…LExd4 2.cxb8=LE#!, 1…PAxd4 2.cxb8=PA#! A Task on the theme “Promotion-unpin-selfpin” that has a demonstration effect. Here the number of thematic variations can increase if other fairy pieces are placed on the board!

b) En-Passant capture is impossible!

In Disparate (Py) the En-Passant capture is always illegal, because in making a move, the Pawn paralyses the opponent’s Pawn!

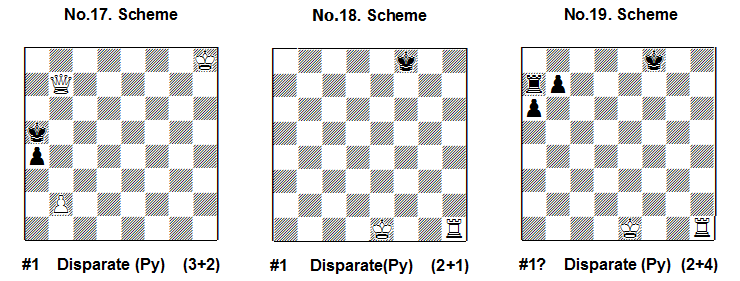
In other words, Disparate is “Play without En-Passant”! For this reason in Scheme No.17 there follows 1.b4#, because Pa4 is paralysed and the capture 1…axb3 is illegal!

c) Castling

The Disparate(Py) rule for castling (if all other rules from orthodox composition are satisfied) is simple. This move is realised also with King and Rook simultaneously, but it is perceived only as a King’s move!

Therefore, after 0-0 or 0-0-0 only the King which realises the castling can paralyse (HMP) the enemy King! The castling Rook which has a «50% role» in this strange move, cannot paralyse an enemy Rook!

In Scheme No.18 after 1.0-0 Black is mated because the black King comes under check from Rf1 and it is paralysed by the white King!

But in Scheme No.19 there is no immediate mate: 1.0-0+? because Kf8 is paralysed but Ra7 is not paralysed and there follows 1…Ra8!! with paralysis of Rf1!

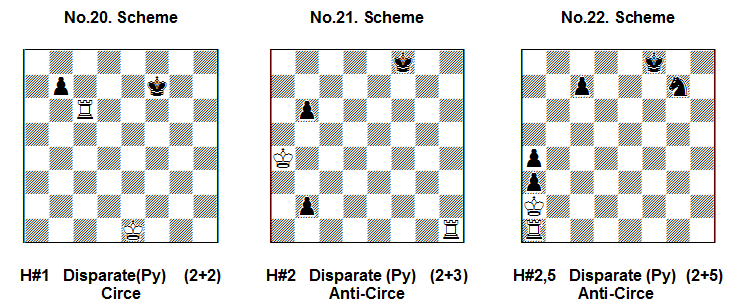
Castling with the help of Circe (Anti-Circe, and other analogical circe kinds) with reborn Rook or King is also possible: No.20. 1.bxc6(Rh1) 0-0#; No.21: 1.b5+ Kxb5(Ke1) 2.b1=S! 0-0#.

Also permitted is castling after rebirth of both pieces – King and Rook that occurs on e1/h1 but only according to different Circe (Anti-Circe, еtc) rules: No.22: 1…Kxa3(Ke1) 2.Se6 Rxa4(Rh1) 3.Sc5 0-0#. Here 1.Ra1? fails because it is not an Anti-Circe move but only an orthodox R-move!!

d) Paralysis between different kinds of Pawns

1. According to the rules of Disparate(Py) paralysis between different kinds of Pawns (royal or not royal) is impossible.  For example: a white (neutral, half-neutral, etc.) Pawn cannot paralyse an enemy  black (neutral, half-neutral,etc) Berolina Pawn, Super Pawn etc. and vice versa!

2. But do not forget that these different types of Pawns can be promoted in a uniform way – to orthodox pieces Queen, Rook, Bishop, Knight or to fairy pieces that are present on the board, for example: Grasshopper, Nightrider, etc.  Therefore, only after such promotions is Disparate-paralysis possible between pieces of the same  type “x”.

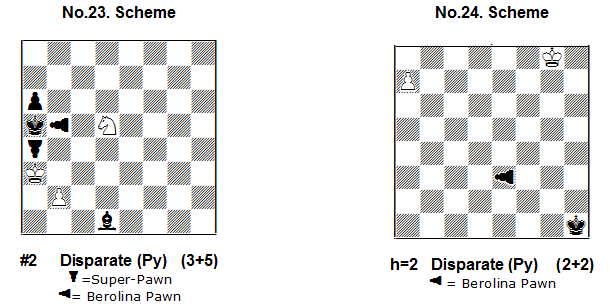
In Scheme No.23 after 1.b4+! Black answers with 1…BPxb4 and there follows the already known Disparate mate 2.Kxb4#. An interesting question – is there possible a variant 1…SPxb3(e.p.) 2.Ka4#? The answer is no, because here the en-passant capture is not possible – despite the fact that after White’s key-move the SPa4 is not paralysed by Pb4!
In Chess composition  en-passant capture is possible only between orthodox Pawns where the movement of these Pawns is not hindered by additional fairy conditions!

In Scheme No.24 paralysis between Pa7 and Berolina Pawn e3 is impossible, therefore we can play 1. BPf2 a8=R! 2.BPg1=R+! But now we have on the board two orthodox Rooks – white and black, and a Disparate paralysis is legal after 2…Ra2=!.

e) Play with Royal pieces

The main rules:
1. According to Disparate (Py) condition, a royal piece of type “x” can paralyze only an enemy piece of the same type “x” (royal or not royal) and vice versa.
2. Neutral (half-neutral, etc) pieces of type “x” (royal or not royal) can be paralysed by both sides after moves of an enemy piece (royal or not royal) of the same kind “x”.
3. An orthodox King cannot paralyse an enemy royal piece of type “x” and vice versa.
4. A royal pawn can be promoted to different kinds of royal pieces.

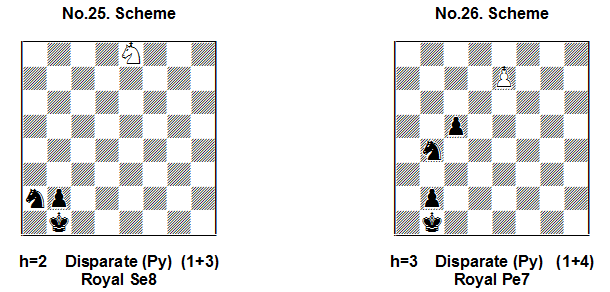
In Scheme No.25 the rSe8 can paralyse Sa2 but cannot paralyse the black King. For this reason a blockade of the black King is needed: 1. Ka1 rSd6 2.b1=S! rSc4 =! A finale with two paralysed black S by the white rS!

Scheme No.26 is a variation of the previous position – here a royal pawn is used. Of course, a promotion to white rS is needed but also very important is the right sequence o black moves! 1.Sa2! e8=rS! 2.Ka1! rSd6 3.b1=S rSc4=. False is 1.Ka1? e8=nS and now Pb2 is paralysed, on the other hand not possible is 2.Sa2? and rSe8 is paralysed!

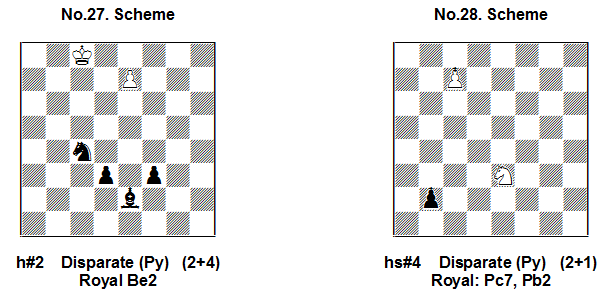
In Scheme No.27 the promoted w.B paralyses the black royal B: 1.rBd1! e8=B! 2.Se5!! (tempo-move!) 2…Ba4#! Wrong is 1. Se5? e8=B 2.rBd1? and now Be8 is paralysed and 2…Ba4# is impossible. Of course, after 1.rBd1 e8=B tempo-moves with Pd3 and Pf3 are impossible because these pawns are paralysed after the promotion of the white Pawn! For the same reason it is wrong to start with 1.d2? or 1.f2? and Pe7 is paralysed!

Scheme No.28 demonstrates Royal Pawns’ promotions into two royal pieces of type “x” (Bishops): as 1.rPc8= rB? is wrong (rPb2 is paralysed) White must begin with the Knight: 1.Sc4 + rPb1=rB! 2.Sa5 rBe4 3.rPc8=rB! rBa8 4.Sb7 rBxb7# (rBc8 is paralysed)!

f) Paralysis between Chameleons

The main rules:
1. A Chameleon (royal or not royal)  in phase  “x” , where “x” can be CQ, CR, CB or CS, can paralyse after its move an enemy Chameleon which stands on the board also in phase “x” or/plus an enemy piece  (royal or not royal) of type “x”!  After its paralysing move the Chameleon in phase “x” gets a new phase “y” in accordance with the rules for moving Chameleons. Thus, the paradoxical point here is that in the final position  the paralysed enemy Chameleon remains in phase  “x” but the paralysing Chameleon after its move has already  a new phase “y”! 
2. When making a move, a  piece (but not Chameleon!)  of type “x” can paralyse an enemy Chameleon that stands on the board in the same phase “x”!
3. But if making a move and becoming a new phase “x”,  a Chameleon cannot paralyse an enemy Chameleon in phase “x” or an enemy  piece of type “x”! 
4. These principles are also valid for play with neutral pieces, half-neutral pieces etc.

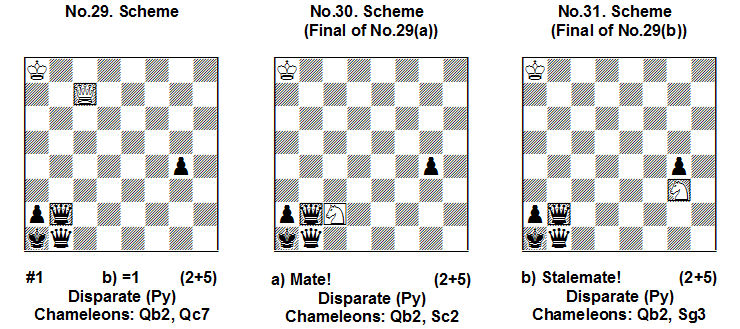
In Scheme No.29 the Chameleon’s phase “x” is  Queen (CQ). The pieces CQb2 and CQc7 have the same phase “x” (CQ). Therefore, after its move CQc7  paralyses  Qb1 and CQb2. In position a) we have:  1.CQc2=CS#!! Pay attention that in the final position the black Chameleon remains in Q-phase (“x”)  but the mating white Chameleon changes phase to a new  one – CS (“y”) – Scheme No.30.
In position b) the play is analogical: 1.CQg3=CS = stalemate because Qb1 and CQb2 are paralysed – Scheme No.31.

Of educational character is the light problem  No.32.  Set-play: 1…e8=CS!! 2.CQa2=CS! Now both Chameleons have the same phase “x” (CS)  and there follows: 2…CSf6=CB#!  because CSa2 is paralysed by CBf6. But it is interesting that Black cannot retain this play, having no tempo-move! In the real play the solution seems difficult: 1.CQc4=CS! e8=CB!! 2.CSb2=CB! – now all pieces on the board (except the King and pawn, of course)  have “x” (B) phase. Therefore, we can play 2…CBa4=CR#!! with paralysis of CBb2 and Bb1! Model-mates in both phases.

No.33 shows another type of change of promotions – an orthodox piece in one phase and chameleon-piece in another phase. Set-play: 1….a8=CR!! 2. Cbb1=CR+! CRh8=CQ#! Real play: 1. CBc2=CR! a8=Q! 2.CRb2=CQ+! Qh1#!

In No.34 we can plan mates as CQc1=CS#, CRb1=CQ#, CBe3=CR# and CSf1=CB#. But in the initial position, these moves do not lead to the goal: 1.CQc1=CS+? Sc6~! and the black S paralyses the white CS! Analogically: 1.CRb1=CQ+? Qc8~!; 1.CBe3=CR+? Ra5~!; 1.CSf1=CB+? Bg8~!. A good idea is to sacrifice black Q,R,B,S: I. 1.Sb4 2.Sa2 3.Sc1! CQxc1=CS#; II. 1.Qg4 2.Qd1 3.Qb1! CRxb1=CQ#; III. 1.Ra7 2.Re7 3.Re3! CBxe3=CR#; IV. 1.Be6 2.Bh3 3.Bf!1 CSxf1=CB#.

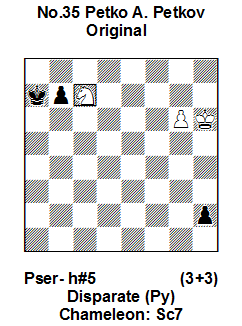
Many interesting ideas may be realised using the stipulations “Pser”, “Phser, etc. The miniature No.35  demonstrates two surprising promotions to CQ with a full Chameleon-cycle of the black promoted CQ and bicolor Bristol CQ/CQ on the final move: 1.h1=CQ+! Kg7! 2.CQh5=CS+ Kh8! 3.CSf6=CB+ g7 4.CBd8=CR+! g8=CQ!! 5.CQb8!! CQc8=CS# with paralysis of CQb8 by CSc8 and model mate!  Can Black achieve the goal through a banal series of  K – moves, for example: 1.Kb6 2.Kc5 3.Kd6 4.Ke5 5.Kf6? The answer is no, because after 5.Kf6 the w.K is paralysed by its black opponent and it is not possible to mate with 5…Kg7(g5).

End of Part I. The next two parts will be published soon.

PART II – Play with neutral (halfneutral, etc) pieces (will be published soon!)

PART III – Disparate in combination with other conditions (to be published…)