No.345 (JV)

No.345 by Julia Vysotska – Anti-batteries, reciprocal play of neutral PAO/NAO, Take&Make with activity of the white King and black Q! (JV)

Definition:

PAO(PA): Moves as Rook, but captures only by hopping over a hurdle to any square beyond.

NAO(NA): Moves as Leo, but on Nightrider-lines instead of Queen-lines.

Nightrider(N): A Rider along a straight line on squares lying a Knight`s move away from each other.

Take & Make: Having captured, a unit must immediately, as part of its move, play a non-capturing move in imitation of the captured unit from the capture-square. If no such move is available, the capture is illegal. Promotion by capture occurs only when a pawn arrives on the promotion rank as the result of a take&make move. Checks are as in normal chess: after the notional capture of the checked K, the checking unit does not move away from the K’s square.

No.345 Julia Vysotska Latvia original-06.07.2013 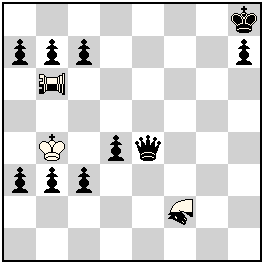  h#2,5          2 solutions        (1+10+2) Take&Make Neutral Pao b6; Nao f2     Solutions: (click to show/hide)   I. 1…nPAb6-f6 2.Qe4-f5 nPAf6×f2-c8 3.Qf5-c5 + Kb4×c5-f8 # II. 1…nNAf2-h3 2.Qe4-d5 nNAh3×b6-b5 3.Qd5-c4 + Kb4×c4-f7 # (C+ by Popeye 4.63 and WinChloe 3.24)   This problem is partly based on the idea shown in my problem No.342(Julia’s Fairies – 2013/II). Anti-batteries created with neutral PAO/NAO and a white King as a forward piece, where all pieces move to their positions using Take&Make condition. Reciprocal play nPAO & nNAO: in (I) neutral PAO makes a first move to come to the position from where it can capture neutral NAO and to move in accordance with Take&Make condition to the position of anti-battery’s rear piece; in (II) neutral NAO makes a first move to come to the position from where it can capture neutral PAO and to move in accordance with Take&Make condition to the position of anti-battery’s rear piece. Black Q on its first move creates a hurdle for neutral PAO/NAO for capturing of each other; and on its second move it is sacrificed to the white King with an “Attraction” motive – the wK moves by Take&Make and occupies a thematic square, creating an anti-battery as a forward generic levitra with dapoxetine piece. (Author)