|
|
Updates as of 06-May-2012:
|
Block of Neutral Battery Piece – I
 |
BLOCK OF NEUTRAL BATTERY-PIECE(Part I)IGM PETKO PETKOV |
 |
I. INTRODUCTION
There’s one very simple, but interesting fairy idea, which might be called also the theme: block of neutral piece, which participates in a battery creation. Different variations of such batteries are possible – the neutral piece there, let’s call it “X”, can be either a forward piece, or also rear piece.
Of course, the idea can be realised in the anti-battery play as well. It should be specially mentioned, that all these possibilities are studied and used in a practise a very little yet.
But why our “Х” should be blocked during the process? The answer is simple: it should be blocked, to not allow to the side, which gets mate, to go away – to make a move with “X” to avoid the mate. Or, in the other words, the piece “X” which is blocked with the aim – to prevent its leaving of the battery-line. Also, some special situations exist, where the piece “X” has to be blocked to prevent it from the giving a check to the opposite King, when it leaves the battery-line (such moments might happen in a case, when the neutral Locust piece is used as a piece “X”).
This article is planned as a material of the numerous parts, and at the same time it is intended to the both – to the masters in composition, and also to the beginners. For these reason many of thematic effects here in the beginning are demonstrated with the simple positions – the schemes, where the only one option or solution is possible. Also, many works of the masters of Fairy genre will be presented later in the article, after the starting material will be well-learned. Of course, the theme Block of the Neutral Battery Piece can be used in all genres of composition, in other words – for all the stipulations, which determine the aim of a play: direct mates, helpmates, selfmates, and also help-selfmates. It is possible also to realize this theme in a fairy problems with almost any of fairy conditions: Circe, Madrasi, Andernach, Take&Make etc. But in the 1st part of this material we’ll look only at the problems without additional fairy conditions which will be discussed at the very end of this cycle of articles.
Probably, the reader immediately will notice, that the theme we are reviewing, almost always are developed in conjunctions with other themes or ideas. And the richer is this synthesis, the better is the result! But at the beginning the examples will be very simple to be understandable for any reader who is familiar with the neutral pieces.
II. TYPICAL EFFECTS
So, let’s start from the simple effects of the blocks used in direct and indirect batteries. Now the series of the elementary schemes will be shown, but it is important to learn the methods of the blocks here very well as in the future it will be very much needed!
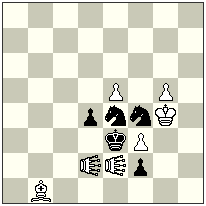
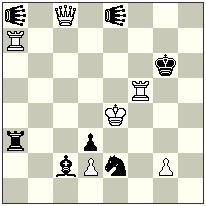
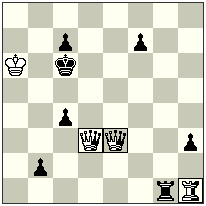
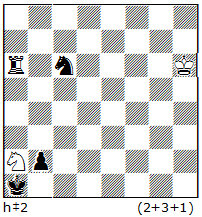
No.1. Scheme
No.1
White can’t give mate right after 1. Rf8+?? because black has a strong defense: 1….nBh2! – neutral bishop simply leaves the battery-line, and white is unable to remove this protection. But how it is possible to realise H#2 here? Of course, a simple analysis shows, that it is possible to do so in a case if black will block the square h2 for the neutral bishop. It’s easy to see how it can be done: 1. Sf1! Kb5 (this is a tempo-move of white!) 2.Sh2 Rf8#.
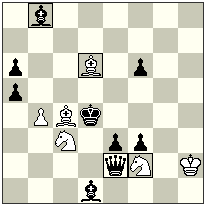
No.2
It’s also not very simple thing to give a mate from the battery on the vertical “a” as the rear piece of this battery is a neutral rook. For example, if we try 1.Sd8+? K~ – then the battery is absolutely useless – for the move 2…Sc3+? the neutral rook simply goes away along the 6th horizontal, f.i. 3.nRb6! ОК. Then we have the only possibility – to block (if it is possible!) the neutral rook and to give a mate like in the example No.1.
This is how it can be done: 1. Sd4+!! Ra3!! – only this move works –the rook is prepared for the future block! 2.Sb3!! – the neutral rook is already blocked and 2…Sc3# follows, as the rook can’t leave the battery line anymore to avoid the mate.
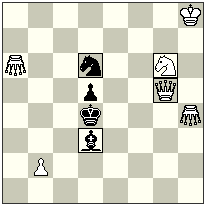
No.2. Scheme
Please pay your attention to this interesting idea – although, this is in the one solution only, but plays 2 “combined batteries”: the 1st one is black-neutral Sc6/nRa6 —along the 6th horizontal, and the 2nd one is white-neutral Sa2/nRa6 – along the vertical “a”.
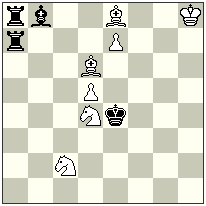
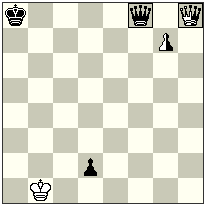
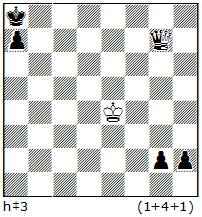
No.3
It is surprising, that the blocked piece can be even the neutral Queen, if it is a rear piece of the battery.
The mate is achieved after the masked battery K/Q creation in a following way: 1.nQa1 Kd5 2.nQh1 Kc6 3.g1=B+ c7# – the thematic black move here is 3.g1=B+ but the method of limiting the mobility of the neutral Q, moving it to the corner of the board, is very important for practical purposes.
No.3. Scheme
Of course, it’s possible to bloack also many fairy pieces, which participate in a batteries or anti-batteries.
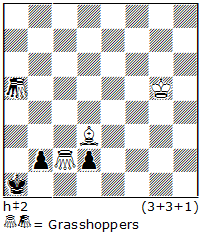
No.4.
The plan of white here is to move a bishop to a2 square, and, building an anti-battery, give a mate. But the realisation of this idea is prevented by running away of the nGa5 to h5: 1. ~ Bc4 2. ~ Ba2+? , but 3. nGh5!! That’s why the black blocks the squares in an interesting way: 1.d1=B Bc4 2.Bh5 Ba2#! – now nGh5 is not possible anymore.
No.4. Scheme
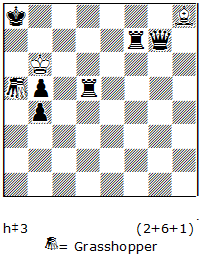
No.5.
The aim of the white here is to build the anti-battery on the vertical “a” using nGa5 (the rear piece) and the white bishop (the forward piece). But to achieve this goal it is needed to block totally all the 3 fields which nGa5 can use to run away: c3, c5, c7. This is how it can be possible: 1.Qc3 Be5 2.Rc5 Bb8 3.Rc7 Ba7#.
No.5. Scheme
In all previous examples we were looking at the block of the rear battery-piece. But in a battery or anti-battery we can block also a forward battery-piece. The next schemes will show the typical effects of such blocks. Btw, not all the fairy pieces can be used to realize this kind of block. What you have to do here – is to choose the right fairy piece which can play the thematic role!
No.6. Scheme
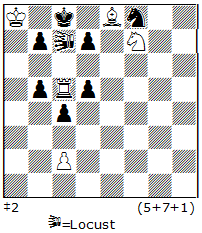
No.6.
Here in the beginning we have a battery of the Rc5 (rear piece) and nLOc7 (forward piece). But the tries to give mate in 1 one doesn’t work, f.i.: 1.nLOxb7-a7+? but 1…nLOxc5-d4!; 1.nLOxd7-e7+? but 1…nLOxc5-b4! The effect of the neutral piece, which captures the another battery-piece as a defense, is shown very well here – and this is the useful effect which has to be learned!
The solution: 1.c3! – zugzwang. Now please look at the following options: 1…d4 2n.LOxb7-a7#! — the mate is already possible as the black pawn had blocked the square d4 for the neutral locust and it can’t capture the rook! Analogically: 1…b4 2.nLOxd7-e7# — because now the square b4 is blocked. The additional options are: 1…d6 2n.LOxd6-e5#, 1…b6 2.nLOxb6-a5#, 1…S~ 2.Bxd7#
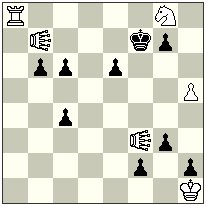
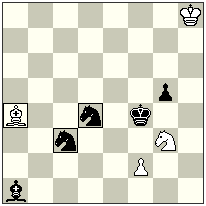
No.7.
A try to build an anti-battery here 1.nLOхb4-b5+? – doesn’t work at the beginning, as black can answer in 2 ways: 1…nLxe2-f1+! and 1.nLOxd5-e5! The solution is clear — it is needed to block the squares f1 and e5 for the neutral Locust. This is how it can be done: 1.Bf4! Kf1! 2.Be5! nLOxb4-b5#.
No.7. Scheme
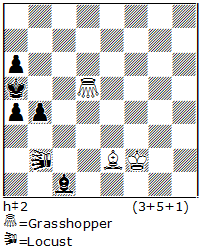
Please note the different methods of blocking — in one case the square е5 is blocked by the black, in another — the square f1 is blocked by the white. Consequently, in some cases – especially using the neutral Locust! — the possibility of thematic block has the both sides!
So far we have discussed the schemes only, and probably some of the readers might think, that it is complicated to compose an interesting problems here. But this is not really so, as the next example shows.
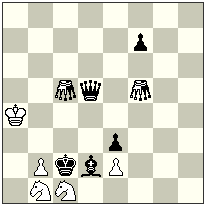
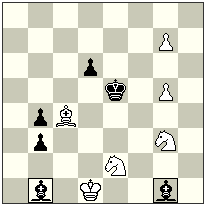
No.8.
At the beginning let’s see how the play will look from the white’s move: 1…Lia3 2.Sc4! nLOxc4-c3#! The idea of the combination is clear: the white Lion blocks the neutral Locust, which after the mating move can’t give a check to the white King as the square а3 is blocked! Of course, with the sacrifice of black S, the black has created an opportunity for the neutral Locust to show it strength as an opening battery-piece of nLO/Li.
No.8. Petko Petkov
original
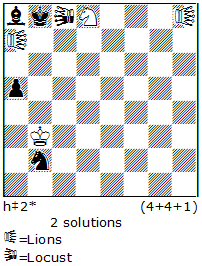
But here is black to move and because of zugzwang it is impossible to keep a set-play. So, the new play is needed! It is possible, realizing the analogical thematic: I. 1.Sd3 Lia2 2.Sc5+ nLOxc5-c4#; II. 1.Sd1 Lia4 2.Sc3 nLOxc3-c2#. Three-phase play between the Lion and the neutral Locust here has a form of duel, and an important additional motive: the black S is three times sacrificed on different squares!
In the next part we’ll look at more complicated examples with the battery-pieces like Chameleons, Chinese pieces etc.
To be continued…
NEW Section! Original Problems
 |
28 April, 2012I’d like to present the new section at JuliasFairies:Original Problems
|
JuliasFaries Announcement
 |
28 April, 2012Several announcements of the site:
|
RE: Kangaroo or Lion?
 |
It’s a great pleasure for me to present the following comment to the post “Kangaroo or Lion?” from the 23rd of April, 2012, and to the further discussion, by IGM Petko Petkov |
Kangaroo or Lion? |
|
VARIATIONS OF ONE THEME
Igm PETKO PETKOV
Problem No. 4 is a very interesting work from Julia! My congratulations to her, about this nice h#2 whose mechanism is very rich and many modifications are possible here! Julia`s opus provokes also some important theoretical questions which deserve attention in practical aspect. (By the way, I accept Diyan`s proposal to change w.Pe5 with bl. Pe5).
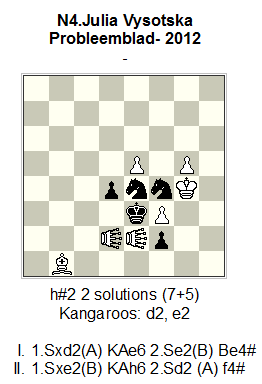
The author defines the thematic complex so: “Zilahi, Umnov, Critical KA-moves, cycle AB-BA of black self-block moves, creation of anti-batteries”.
OK, but here is needed to add: “Line-opening for white Kangaroos after black S-moves”.
The main theme of Julia`s problem is possible to define so: “A black piece “X” blocks square around the black King and simultaneously opens line for white piece “Y” (from Hoppers-type). “Y” makes a critical move and then White creates an anti-battery and gives mate”.
This complex, which reminds a classical “Indian theme”, is sufficiently difficult and interesting and it can be an independent theme in many other problems.
Therefore, I recommend to the readers to apply this theme in theirs own compositions, using different fairy pieces from Hopper`s type!
But let we return again to No. 4. Here the author marks also other motives: cycle AB-BA of black moves and theme “Zilahi”. A special attention deserves the question about “Zilahi”. In my opinion, here we have only “Half-Zilahi” (we can say also “Partial Zilahi”)!
My argumentation: here the mates follow after play of anti-batteries. But every anti-battery is constructed from two pieces: forward battery-piece (every kind of piece can execute this function) and rear battery-piece (only Hopper-piece can execute this function). For example: in I solution: I. 1.Sxd2(A) KAe6 2.Se2(B) Be4# the forward piece is the white Bishop but the rear piece is the white Kangaroo. The joint play of these figures follow to mate.
But attention! Here Black captures only one of these pieces – white Kangaroo! Therefore there is only “half” Zilahi effect. A whole Zilahi-effect would be possible only if Black captured the both white battery-pieces!
This argumentation must be valid also for standard direct or indirect batteries.
Two Kangaroos, or only one?
According to Seetharaman`s proposal
seetharaman says:
April 23, 2012 at 9:13 pm
With the experts joining, this discussion is proving to be very interesting and educative. I have one question for the experts:
Suppose in Version 4, we remove Kangaroo e2. Now the problem can be twin (a) Diagram. (b) Move d2 to e2. The theme, play and content are unchanged. Would you prefer the twin setting with one Kangaroo less, or use two white Kangaroos for “multi solution” form ?Similar twinning possible for version 4.1 also.
N 4 can be modify to the following version – 4A :
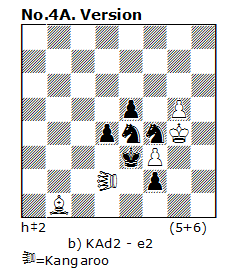
Here we have of course one Kangaroo less but there is in N 4A no “Half-Zilahi”. In my opinion here the choice between N 4 and N 4A can be a subjective estimate of author.
Myself I think that the version with both Kangaroos and 2 solutions is better. Speaking for economy as the main principle in Chess composition, we cannot perceive this principle as a fanatic postulate which always should be interpreted as much as possible strictly. Between two Kangaroos in N4 exists a functional thematic subordination and it is not desirable to break this important effect which have also aesthetical value.
Whether the Lion is better?
seetharaman says:
April 22, 2012 at 5:35 pm
Excellent imagination to show different effects with the similar settings of Nos.4 and 6. Can No.4 be more economical if Lions are used instead of Kangaroo.?
Julia`s answer:
About the Lions: Yes, I can take off the white pawns (e5, g5) in case of Lions, but at the same time I won’t need to block the squares e2/d2 on the blacks’ second move. So, have to find some other idea for this move.For now I’ve composed 2 versions of the problem No.4 – with Lions (4.1) and with neutrals: Bishop-Lion and Rook-Lion (4.2).Of course, some more motivations are possible to the black knights on the 2nd move.

I quite agree with Julia’s opinion that in this scheme the application of Lions instead of Kangaroo changes thematic complex. N 4.1 and N 4.2 are good problems of course but here exist also some important theoretical & practical questions.
At first it is possible, for example, to change the “Queen”-Lions in 4.1 with Rook-Lion and Bishop-Lion without any other thematic modifications – Version N 4B.
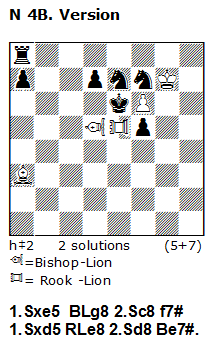
A simple rule, which have also subjective character: We should use always Rook-Lion(s) and Bishop-Lion (s) if the use of Queen-Lion (s) is not needed!
The same rule is valid also for Kangaroos! We can define therefore three kind of Kangaroos: Queen`s Kangaroo (the well known standard type) , Rook-Kanagoo (plays only on Rook-lines) and Bishop-Kangaroo (plays only on Bishop-Lines).
Therefore, in N4 we can change both Queen`s Kangaroos with theirs modifications: N 4C
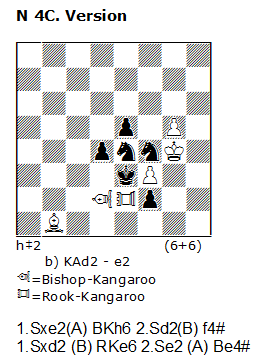
But what says the solver?
Changing Queen`s Lion or Queen`s Kangaroo with theirs slighter analogs, we submit an economy principle. OK. But this “thrift of power” has also negative effect.
As common conclusion we can say, that all pieces from type “Hoppers” are figures with rather limited mobility. Often on a diagram such pieces even cannot play, as Bishop-Kangaroo on the square “d2” in position 4C, for example. Here also Rook-Kangaroo on “e2” is almost immovable – it can play only on “e5”. In our basic problem – N 4 from Julia, every white Kangaroo has only one move: KAd2 – to g2, and KAe2 – to h5.
Such strong limited or full limited mobility of Hoppers in every case means an easy solution, of course, if the “move-distance” is short (2 moves) and the position is not heavy. Such compositions are a “facile drink” for the solvers, from other side, the strong limited mobility of Hoppers is obviously a negative fact in aesthetical attitude.
In my opinion, all these negative effects in one or in other degree exist in problems with short number of moves and especially – in help-genres.
In this relation I can make the following general recommendation: if it is possible, compose Your problems in 2,5, 3 or more moves, in which yours Hopper –pieces have more possibilities for play. An interesting chance in this aspect is application of neutral or half-neutral pieces.
Award of KoBulChess TT 2012

I’m happy to anounce the following event as of April, 23, 2012:
Kobulchess.com presents theAward of the KoBulChess TT 2012 by Diyan KostadinovVisit Kobulchess.com to see the whole award! |
|
Award of KoBulChess TT 2012
 I was very pleased to receive a total of 74 problems by 17 authors from 11 countries for the 1st KoBulChess TT 2012. The level of the tourney is high with so many entries with original and interesting thematic complexes!
I was very pleased to receive a total of 74 problems by 17 authors from 11 countries for the 1st KoBulChess TT 2012. The level of the tourney is high with so many entries with original and interesting thematic complexes!
In the announcement of the tourney I was written that the tourney consist of 2 sections:
Section A: KoBul Kings problems without any other fairy pieces or conditions.
Section B: KoBul Kings problems with fairy pieces (no other fairy conditions were allowed).
I had received so many miniatures, so finally I’ve decided to split the first Section, to separate a section for the miniatures. So the award is split into the following sections:
-section A1: direct #/=, H#/=, S#/=, HS#/= problems in 2-3 moves and 7+ pieces with white / black KoBul Kings without fairy pieces or another fairy conditions;
-section A2: direct #/=, H#/=, S#/=, HS#/= miniatures in 2-3 moves with white / black KoBul Kings without fairy pieces or another fairy conditions
–section B: direct #/=, H#/=, S#/=, HS#/= problems in 2-3 moves with white/black/neutral KoBul Kings with other fairy pieces, but other fairy conditions are not allowed.
Definition: KoBul Kings – When a piece (not a pawn) of his own side is captured, a King transforms into a Royal piece of the same type as the captured one. When the King is in the form of any Royal piece and there is a capture of one of the pawns of his own side, he becomes a normal King again.
Captures are illegal if they result in self-check by the transformed King. Castling is allowed only if the KoBul King is on his initial square in the form of a normal King and if he has not already moved; however he may already have been transformed. In the case of capture by a King in AntiCirce he is reborn on his initial square and may castle. If the capture is by a King which is in the form of some Royal piece, he is reborn on the initial square of that piece.
Participants: Pierre Tritten, Petko Petkov, Velko Aleksandrov, Juraj Lorinc, Vlaicu Crisan, Eric Huber, Kostas Prentos, Emmanuel Manolas, Themis Argirakopoulos, Ioannis Garoufalidis, Manfred Rittirsch, Julia Vysotska, Luis Miguel Martin, Jacques Rotenberg, S.K.Balasubramanian, K.Seetharaman, Cornel Pacurar.
Visit Kobulchess.com to see the whole award!
Kangaroo or Lion ?
 |
April 22, 2012Kangaroo or Lion ?This post is an anwer to the comment on The Main Accent: BATTERY-PLAY:
|
| First of all – thank you very much for your deep analysis and your ideas! I appreciate your comments a lot! About the Lions: Yes, I can take off the white pawns (e5, g5) in case of Lions, but at the same time I won’t need to block the squares e2/d2 on the blacks’ second move. So, have to find some other idea for this move. For now I’ve composed 2 versions of the problem No.4 – with Lions (4.1) and with neutrals: Bishop-Lion and Rook-Lion (4.2). Of course, some more motivations are possible to the black knights on the 2nd move. |
No.4
Julia Vysotska
Probleemblad- 2012
–
h#2 2 solutions (7+5)
Kangaroos: d2, e2
–
I. 1.Sxd2(A) KAe6 2.Se2(B) Be4#
II. 1.Sxe2(B) KAh6 2.Sd2 (A) f4#
–
Zilahi, Umnov, Critical KA-moves, cycle AB-BA of black self-block moves, creation of anti-batteries, Meredith.
|
|
No.4.1
Julia Vysotska
Version 4.1
–
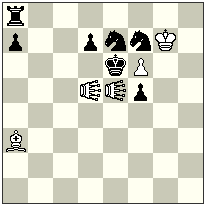 h#2 2 solutions (5+7) h#2 2 solutions (5+7)Lions: d5,e5
–
I. 1.Sxd5 LIe8 2.Sd8 Be7 #
II. 1.Sxe5 LIg8 2.Sc8 f7 #
–
Here the black knights on the 2nd move don’t block the King (as in No.4), but close the line of Ra8. The other thematic is the same.
|
No.4.2
Julia Vysotska
Version 4.2
–
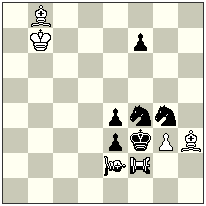 h#2 2 solutions (4+6+2) h#2 2 solutions (4+6+2)Neutrals: Bishop-Lion e2, Rook-Lion f2
–
I. 1.Sxe2 nRLf5 2.Sf6 Bf4 #
II. 1.Sxf2 nBLh5 2.Sg6 g4 #
–
Here the black knights on the 2nd move don’t block the King (as in No.4), close the lines for neutral BL/RL so these pieces can’t go away on the mating move. The other thematic is the same.
|
The Main Accent: BATTERY-PLAY
Some comments about the battery-play in the problems below
In the future posts I’ll write more about these and some other non-standard themes and ideas which figure in my unobtrusive fairy-repertoire..
1. Helpmates
|
No.1
Julia Vysotska
The 14th Sabra TT – 2011
Commendation
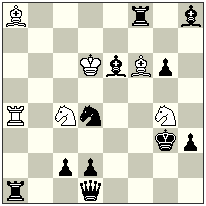 h#2 2 solutions (6+11) h#2 2 solutions (6+11)–
I. 1.Sf3 Se3(1…Sxd2?) 2.Se1 Sf1#
II. 1.Bxc4 Bxd4 2.Bf7 Bf2#
–
ANI-problem: 2 solutions with anti-identical contents in thematic attitude; the both Knights (Sc4/Sd4) which are captured in the first phase, make all half-moves in the second phase; annihilation captures on c4/d4; Bivalve-theme realized by Be6/Sd4; a try with S-self-pin in the first solution; an additional line-opening for Rf8 executed by the wBf6 in the second solution.
–
This is really the 2nd my problem, composed during the nights of 22-23rd of August, 2011, for Sabra Tourney in Jesi.
|
No.2
Julia Vysotska
The Problemist Supplement – 2012
–
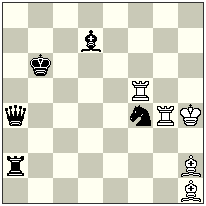 h#2 2 solutions (5+5) h#2 2 solutions (5+5)–
I. 1.Se2 Re4 2.Kc6 Rb4 #
II. 1.Se6 Be5 2.Kc5 Bc7 #
–
Bivalve with additional line-opening for the white forward piece which creates a battery. Aristokrat-problem.
–
|
2. Fairies
|
No.3
Julia Vysotska
Уральский Проблемист – 2012
–
hs#3 b) +bSb8 (7+4)
–
a) 1.Bb5 Bc7+ 2.e8=S Bd8 3.Sf6+ Bxf6#
b)1.Bc6 Sd7+ 2.e8=B Sf8 3.Bg6+ Sxg6#
–
Opening of a black battery-line, white under-promotions, transformation of black B/R battery through replacement of forward piece during battery-line, creation of a Dentist-mechanism. Meredith.
|
No.4
Julia Vysotska
Probleemblad- 2012
–
h#2 2 solutions (7+5) Kangaroos: d2, e2
–
I. 1.Sxd2(A) KAe6 2.Se2(B) Be4#
II. 1.Sxe2(B) KAh6 2.Sd2 (A) f4#
–
Zilahi, Umnov, Critical KA-moves, cycle AB-BA of black self-block moves, creation of anti-batteries, Meredith.
|
No.5
Julia Vysotska
The Problemist – 2012
–
hs#2,5 2 solutions (6+9) Lions b7, f3
–
I. 1… f1=B 2.LIb4 Be2 3.LIf4+ Bxf3#
II. 1… f1=LI 2.LIh3 LIb5 3.LId7+ LIxb7#
–
Creation of reciprocal white anti-batteries (Lion-Lion), black under-promotions, model mates.
|
|
No.6
Julia Vysotska
StrateGems – 2012
–
h#2 2 solutions (5+5+2)
Neutral Grasshoppers: c5, f5
–
I. 1.Q×c5 Sc3(A) 2.Qf8 Sd3#(B)
II. 1.Q×f5 Sd3(B) 2.Qf2 Sc3#(A)
–
Creation of bi-color anti-batteries S/nG, Zilahi theme, distant self-blocks of the neutral Grasshoppers, cycle AB – BA of the white moves. Meredith.
|
No.7
Julia Vysotska
Tehtäväniekka – 2012
–
hs#3 2 solutions (6+7)
Kangaroos: a8, e8
–
I. 1.Rd5 KAf3 2.gxf3 Ra6 3.Qe6+ Rxe6 # (not 4.Re5?? – illegal self-check from KAe8, because of creation of the preventive anti-battery on vertical “e” !)
II. 1.Re5 KAe3 2.dxe3 Ba4 3.Qc6+ Bxc6 # (not 4.Rd5?? – illegal self-check from KAа8, because of creation of the preventive anti-battery on diagonal a8-h1!)
–
Specific mates using Q and KA on the one line, with the impossibility for white to prevent checks because of anti-batteries creation, double white self-block, change of functions of black pieces, reciprocal sacrifices of black KA, model mates.
|
–
My dear readers, I’d appreciate your comments! Also, I’d like to invite you to send your own ideas and problems for this topic – I’d include them into this post.
Sincerely,
Julia
The non-standard Chameleon
 |
April, 2012My start in compositionI want to dedicate the first post on my site to the very first fairy piece I’ve got to know – the Chameleon (type Q-S-B-R-Q). I’d call this piece – my start in composition, as the first problem I’ve composed and even got a Special Prize, was h#2 with Chameleons for The 2nd BULGARIAN WINE Tourney in Jesi, summer-2011. |
The current year, 2012, is also a special year for the Chameleon piece, as this year it celebrates the 50 years anniversary (the first definition of Chameleon with contemporary rules is published in Feenschach, 1962 by Petko A.Petkov, who has developed an old idea). I’m happy to congratulate the inventor of this peace in a way we see it nowadays, famous composer IGM Petko Petkov, with this great date!
I like this piece, a long time known, but still not so much used and studied, as it gives some interesting and non-standard opportunities.
And now – to some of my published problems…. with Chameleons, of course!
–
|
Julia Vysotska
The 2nd Bulgarian Wine TT – 2011
Special Prize
h#2 2 solutions (6+9)
Chameleons: Bd6, Sf2, Bb8, Qe2 –
I. 1.CBc7=CR CBf8=CR 2.CRxc4=CQ CRxf6=CQ#
II. 1.CQa2=CS CSh3=CB 2.CSxc3=CB CBg4=CR# –
The black Chameleons moves on the pin line and unpins the white mating pieces after its transformation. Selfblocks with paradoxical captures of the white pieces, exchange of functions between white thematic pieces, ODT.
|
Julia Vysotska
Strate Gems – 2011
h#2 b) Ga6->c1 (6+4)
Chameleons: Bd3,Sd6,Qg5,Sg6 –
a) 1.CBc4=CR CQg4=CS 2.CSe4=CB CSf2=CB#
b) 1.CSc4=CB CSf4=CB 2.CBe4=CR CBd2=CR# –
Double black self-blocks on c4/e4 realized by the black Chameleons with interchange of functions between them; specific creation of batteries with forward piece Chameleon and rear piece Grasshopper. Interchange of functions between white Chameleons. Meredith.
|
Julia Vysotska
Uralsky Problemist – 2011
h#2,5* (1+3+2)
Chameleons: Qf8,Qh8 –
I. 1.CQd8=CS ng8=nCB 2.CSb7=CB nCBa2=nCR#
II. 1…ng8=ncQ 2.CQc8=CS nCQd8=nCS 3.CSa7=CB nCSc6=nCB# –
Creation of specific Chameleon-batteries in two phases after nPg7 promotions; unpins of black CQ and black self-blocks on b7,a7; bi-color Bristol CQf8 – nQg8 in solution; model mates. Miniature.
|
|
Julia Vysotska
Uralsky Problemist – 2011
h#2 2 solutions (1+7+3)
Chameleons: Qd3,Qe3,Rh2 –
I. 1.Rg8 nCRf2=nCQ 2.Rc8 nCQa7=nCS#
II. 1.Rg6 nCRd2=nCQ 2.Re6 nCQd8=nCS# –
Line-opening after black key-moves, Ambush moves of the nCRh2, black distant self-blocks on c8, e6, specific mates with neutral Chameleons in S-phase. Meredith.
|
Julia Vysotska
Strate Gems – 2012
hs#2 2 solutions (4+5)
Chameleons: Ba4,Sd4,Sc3 –
I. 1.CBe8=cR CSb3=CB (not CSe6?) 2.CRe4=CQ+ CS*e4=CB#
II. 1.CBb5=cR CSa2=cB (not CSd5?) 2.CRf5=CQ+ CS*f5=CB# –
Chameleon half-battery play, dual avoidance with the interference of white chameleon by black chameleon, model mates, Meredith.
|
Julia Vysotska
Strate Gems – 2012
hs#3 2 solutions (6+6)
Chameleons: Bb1,Bg1 –
I. 1.g8=СQ СBh7=СR 2.СQe6=СS СRh1=СQ 3.СSd4=СB+ СBxd4=cR#
II. 1.g8=СR СBa7=СR 2.СRg6=СQ СRa1=СQ 3.СQd3=СS+ СBxd3=СR# –
Creation of reciprocal batteries with 2 chameleons in Bishop phase, white promotions in CQ and CR, model mates.
|